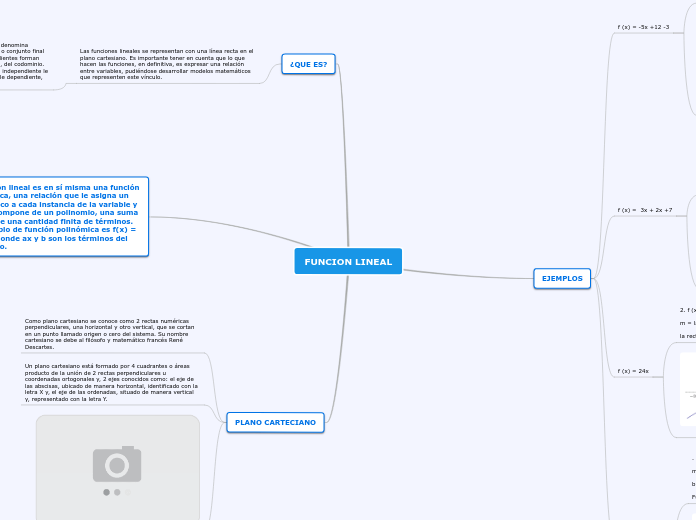
FUNCION LINEAL
PLANO CARTECIANO
Un plano cartesiano está formado por 4 cuadrantes o áreas producto de la unión de 2 rectas perpendiculares u coordenadas ortogonales y, 2 ejes conocidos como: el eje de las abscisas, ubicado de manera horizontal, identificado con la letra X y, el eje de las ordenadas, situado de manera vertical y, representado con la letra Y.
Como plano cartesiano se conoce como 2 rectas numéricas perpendiculares, una horizontal y otro vertical, que se cortan en un punto llamado origen o cero del sistema. Su nombre cartesiano se debe al filósofo y matemático francés René Descartes.
La función lineal es en sí misma una función polinómica, una relación que le asigna un valor único a cada instancia de la variable y que se compone de un polinomio, una suma o resta de una cantidad finita de términos. Un ejemplo de función polinómica es f(x) = ax + b, donde ax y b son los términos del polinomio.
¿QUE ES?
Las funciones lineales se representan con una línea recta en el plano cartesiano. Es importante tener en cuenta que lo que hacen las funciones, en definitiva, es expresar una relación entre variables, pudiéndose desarrollar modelos matemáticos que representen este vínculo.
El conjunto de partida o conjunto inicial se lo denomina dominio, mientras que al conjunto de llegada o conjunto final se lo llama codominio. Las variables independientes forman parte del dominio; las variables dependientes, del codominio. Cuando a los cambios iguales de una variable independiente le corresponden variaciones iguales de la variable dependiente, se habla de función lineal
Y = X + 2 es un ejemplo de función lineal. Supongamos que en el dominio tenemos los valores 2, 5 y 7. Si la función señala que Y es igual a X + 2, en el codominio encontraremos los valores 4, 7 y 9:
X + 2 = Y
2 + 2 = 4
5 + 2 = 7
7 + 2 = 9
EJEMPLOS
f (x) = 5x + 13
. f (x) = 5x + 13
m = la pendiente es 5
b = 13
Funciones lineales ejemplos 1
f (x) = 24x
2. f (x) = 24x
m = la pendiente es 24
la recta no cruza el eje de las y
f (x) = 3x + 2x +7
3. f (x) = 3x + 2x +7
primero simplificamos:
f (x) = 5x +7
m = la pendiente es 5
b = 7
f (x) = -5x +12 -3
Subtema
4. f (x) = -5x +12 -3
primero simplificamos:
f (x) = -5x +9
m = -5
b = 9