FUNCTIONS
The part of speech is a category to which a word is assigned according to its syntactic functions. In English the main parts of speech are noun, pronoun, adjective, determiner, verb, adverb, preposition, conjunction, and interjection.
RESTRICTIONS
A rational expression is a ratio of two polynomials. The domain of a rational expression is all real numbers except those that make the denominator equal to zero
Multiplying and dividing rational expressions
Completely factor all numerators and denominators.
Reduce all common factors.
Either multiply the denominators and numerators or leave the answer in factored form. (if dividing, multiply fractions with a reciprocal)
Adding and subtracting rational expressions
To add or subtract two rational expressions with the same denominator, we simply add or subtract the numerators and write the result over the common denominator. When the denominators are not the same, we must manipulate them so that they become the same.
Functions vs relations (domain and range)
A conjunction is a word like 'if' 'but' or 'and' which is used to connect sentences or clauses together.
Linear Function: f(x) = mx + b.
Square Function: f(x) = x2
Square Root Function: f(x) = √x.
Absolute Value Function: f(x) = |x|
Reciprocal Function. f(x) = 1/x.
The domain is the set of numbers that can be put into a function, and the range is the set of values that come out of the function. So on a standard coordinate grid, the x values are the domain, and the y values are the range.
If you have more than one output for a particular input, then the quantities represent a relation. A graph of a relationship can be shown to be a function using the vertical line test
Coordinating conjunctions always connect phrases, words, and clauses. They are: for, and, nor, but, or, yet, so.
Function notation
A preposition is one of the most exciting parts of grammar. A preposition is used to describe the location of something in relation to something else.
INVERSE FUNCTION
if the function f applied to an input x gives a result of y, then applying its inverse function g to y gives the result x, i.e., g(y) = x if and only if f(x) = y. The inverse function of f is also denoted as f^{-1}.
simpler method of describing a function without a lengthy written explanation. The most frequently used function notation is f(x) which is read as “f” of “x”. In this case, the letter x, placed within the parentheses and the entire symbol f(x), stand for the domain set and range set respectively.
Combining Polynomials
A numeral is a word or phrase that describes a numerical quantity.
Some theories of grammar use the word 'numeral' to refer to cardinal numbers that act as a determiner to specify the quantity of a noun, for example the 'two' in 'two hats'.
you first need to identify the like terms in the polynomials and then combine them according to the correct integer operations. Since like terms must have the same exact variables raised to the same exact power
Simplifying rational expressions
Step 1: Factor both the numerator and denominator of the fraction.
Step 2: Reduce the fraction.
Step 3: Rewrite any remaining expressions in the numerator and denominator.
Step 4: Factor both the numerator and denominator of the fraction.
Factoring - perfect squares
Step 1: Factor out the GCF, if necessary.
Step 2:Write each term as a perfect cube.
Step 3: Identify the given variables.
Step 4:The terms of the binomial are the cube roots of the terms of the original polynomial
Factoring -
difference of squares
An article is a word used to modify a noun, which is a person, place, object, or idea. Technically, an article is an adjective, which is any word that modifies a noun.
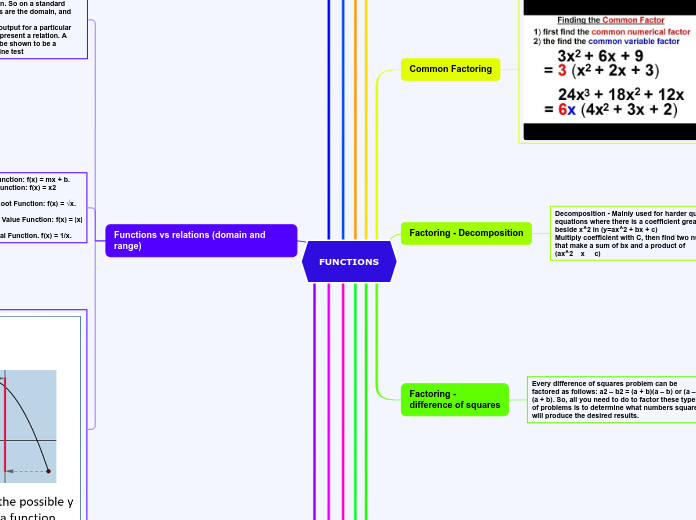
Every difference of squares problem can be factored as follows: a2 – b2 = (a + b)(a – b) or (a – b)(a + b). So, all you need to do to factor these types of problems is to determine what numbers squares will produce the desired results.
It refers directly to a specific noun or groups of nouns.
Factoring - Decomposition
A pronoun is a word that can be used in place of a noun, typically after the noun itself has already been stated.
Decomposition - Mainly used for harder quadratic equations where there is a coefficient greater than 1 beside x^2 in (y=ax^2 + bx + c)
Multiply coefficient with C, then find two numbers that make a sum of bx and a product of
(ax^2 x c)
The personal pronouns are I, you, he, she, it, we, they. More often than not (but certainly not always), they replace nouns representing people.
Common Factoring
An adjective is a word that's used to describe a specific noun and to provide more detail to the listener.
Multiplying Polynomials
A noun is defined as a person, place, thing or idea. Proper nouns always begin with a capital letter. Common nouns, which are general words, such as 'cars,' are not capitalized.
- To multiply two polynomials: multiply each term in one polynomial by each term in the other polynomial. add those answers together, and simplify if needed.
- simply foil out your factored terms by multiplying each term in one trinomial to each term in the other trinomial.
FOIL: first outer inner last
Proper nouns are the names of specific people or places. They should always begin with a capital letter.
Create sentences
Distributive Property
A verb is an action word or 'doing' word that signifies movement in some way.
how to solve expressions in the form of a(b + c)
A verb with its own meaning: a verb that is not an auxiliary verb.