Investigación Operativa I (Capítulo 3 y 4 Taha)

Mer av detta

20 Sucesos Historicos De Las Finanzas

av alejandra linares saucedo

Contrato de compra-venta

av Giancarlo Ferreira

H&M Y LAS TEORÍAS DE RESTRICCIONES

av MARÍA CRUZ CUADRO

FENOMENOS SOCIALES

av Jose david diaz diaz

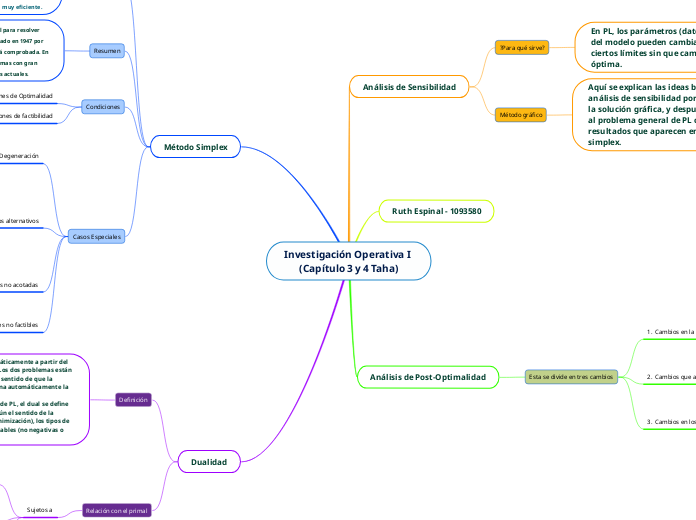
Investigación Operativa I (Capítulo 3 y 4 Taha)

Dualidad

Relación con el primal

Sujetos a

Los coeficientes de la función objetivo en el problema dual, corresponden a los términos independientes de las restricciones, que se ubican del otro lado de las variables (lado derecho)

El número de restricciones que presenta el problema dual se ve determinado por el número de variables que presenta el problema primal.

El número de variables que presenta el problema dual se ve determinado por el numero de restricciones que problema primal.

El problema dual se define sistemáticamente a partir del modelo de PL primal (u original). Los dos problemas están estrechamente relacionados en el sentido de que la solución óptima de uno proporciona automáticamente la solución óptima al otro. En la mayoría de los tratamientos de PL, el dual se define para varias formas del primal según el sentido de la optimización (maximización o minimización), los tipos de restricciones, y el signo de las variables (no negativas o irrestrictas).

Método Simplex

Casos Especiales

Soluciones no factibles

Es un problema que no tiene solución cuando se llega a las condiciones de optimalidad.

Soluciones no acotadas

Son problemas para los cuales una o mas de una de las variables pueden aumentarse indefinidamente, mejorando en forma indefinida la función objetivo.

Óptimos alternativos

Cuando la función objetivo es paralela a una restricción obligatoria, es decir, una restricción que satisface como ecuación en la solución óptima, la FO asumirá el valor óptimo que se satisface como ecuación el solución óptima, en otras palabras, la función objetivo asumirá el mismo valor óptimo.

Degeneración

El problema ocurre en la siguiente iteración donde los valores de una o mas variables básicas llegan a ser cero, en cuyo caso se dice que la soluciones es degenerada.

Condiciones

Condiciones de factibilidad

Condiciones de Optimalidad

Resumen

El método Simplex es un procedimiento general para resolver problemas de programación lineal. Fue desarrollado en 1947 por George Dantzig, y su extraordinaria eficiencia está comprobada. En la actualidad, es utilizado para resolver problemas con gran cantidad de variables, en las computadoras actuales.

Definición

Es un método analítico de solución de problemas de programación lineal, capaz de resolver modelos más complejos que los resueltos con el método gráfico, sin restricciones en el número de variables. Es utilizado en la busca de soluciones donde debemos optimizar recursos de forma muy eficiente.

Análisis de Post-Optimalidad

Esta se divide en tres cambios

Cambios en los coeficientes de la función objetivo

Estos coeficientes cambian la optimalidad y se requiere que se calculen los nuevo coeficientes de la función objetivo o Z.

Cambios que afectan la postoptimalidad

Esta considera la realización de cambios de los coeficientes objetivos y la adición de una nueva actividad económica o variable.

Cambios en la factibilidad

Esta se ve afectada cuando el lado derecho de las restricciones cambia o se agrega una restricción al modelo.

Ruth Espinal - 1093580

Análisis de Sensibilidad

Método gráfico

Aquí se explican las ideas básicas del análisis de sensibilidad por medio de la solución gráfica, y después se extienden al problema general de PL con base en los resultados que aparecen en la tabla simplex.

La sensibilidad de la solución óptima a los cambios en la utilidad unitaria o el costo unitario (coeficientes de la función objetivo).

La sensibilidad de la solución óptima a los cambios de la disponibilidad de los recursos (lado derecho de las restricciones).

?Para qué sirve?

En PL, los parámetros (datos de entrada) del modelo pueden cambiar dentro de ciertos límites sin que cambie la solución óptima.