av daveson lorenzo för 5 årar sedan
272
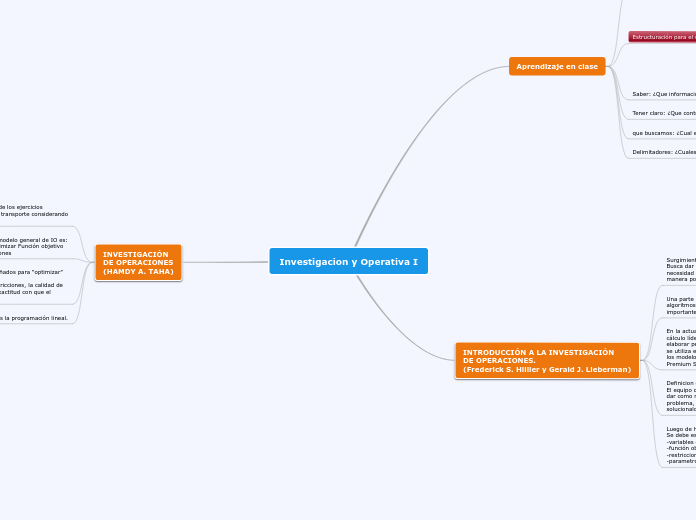
Investigacion y Operativa I
La investigación operativa se centra en la estructuración y resolución de problemas mediante modelos matemáticos. Uno de los enfoques más importantes es la programación lineal, que busca maximizar o minimizar una función objetivo sujeta a restricciones específicas.