av jymmy alexander för 8 årar sedan
245
JYMMY ALEXANDER BOTIA
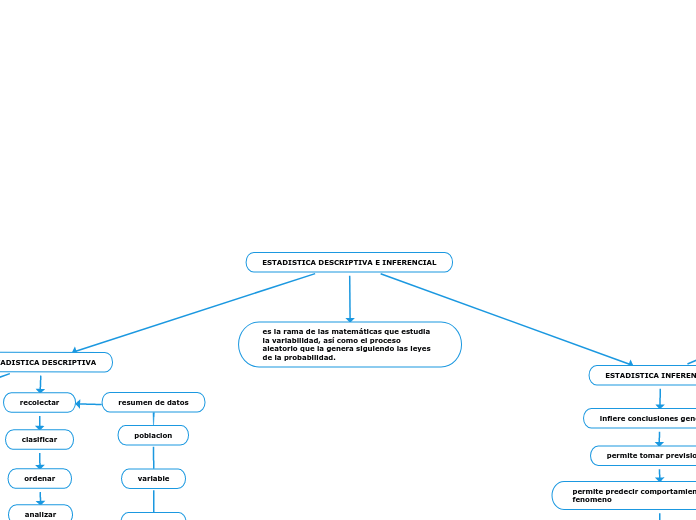
La estadística es vista como una ciencia matemática independiente, con aplicaciones en diversas áreas como la demografía y la economía. A diferencia de las matemáticas puras, la estadística se centra en el análisis de datos y la elaboración de predicciones, intersectando con la teoría de la decisión y la economía.