av Anna Vitale för 3 dagar sedan
18
Mer av detta
Le orbite descritte dai pianeti attorno al Sole sono ellissi con il Sole in uno dei due fuochi
Il modello di Copernico riproduceva le caratteristiche generali dei moti dei pianeti ed era più semplice di quello geocentrico, ma dal punto di vista quantitativo non mostrava un accordo soddisfacente con le osservazioni astronomiche.
Questo difetto fu corretto da Keplero, che ebbe a disposizione la grande quantità di dati sperimentali raccolta a occhio nudo, ma con sorprendente precisione, dal suo maestro Tycho Brahe. Keplero sostenne che le orbite dei pianeti fossero ellissi anziché circonferenze.
Fino al XVII secolo si credeva che la Terra fosse al centro dell'Universo e che il Sole, la Luna e i pianeti le orbitassero attorno. Questo modello geocentrico del cosmo era stato sviluppato da Claudio Tolomeo nel II secolo, sulla base delle idee di Aristotele, già antiche di seicento anni.
Il modello eliocentrico, che toglieva alla Terra la sua posizione privilegiata e poneva Sole al centro, fu proposto da Niccolò Copernico nel 1543 e perfezionato da Giovanni Keplero (1571-1630).
Isaac Newton ipotizzò che la forza gravitazionale che lega la Luna alla Terra e le impedisce di allontanarsi nello spazio, abbia la stessa natura di quella che fa cadere la mela. Nell'idea di Newton questa forza è universale e fa si che due corpi qualunque si attraggano.
La formula F = G * m1*m2/r*r esprime il modulo della forza gravitazionale che agisce tra punti materiali, cioè tra corpi che hanno dimensioni piccole in confronto alla reciproca distanza. È possibile dimostrare, come già fece Newton, che questa formula vale anche per corpi di grandi dimensioni, purché la loro massa sia distribuita in un volume sferico in modo simmetrico rispetto al centro.
I corpi sferici esercitano e subiscono forze gravitazionali come se avessero tutta la massa concentrata nel centro.
La forza gravitazionale dipende dalle masse e dalla distanza reciproca dei corpi interagenti. Secondo la legge di gravitazione universale, formulata da Newton nel 1687,
la forza di attrazione tra due punti materiali di masse m1 e m2 separati da una distanza r, è:
Il modulo di questa forza è:
F = G * m1*m2/r*r
Dove G è la costante di gravitazione universale.
Tenendo fissa la distanza tra i due punti materiali:
Tenendo invece fisse le masse:
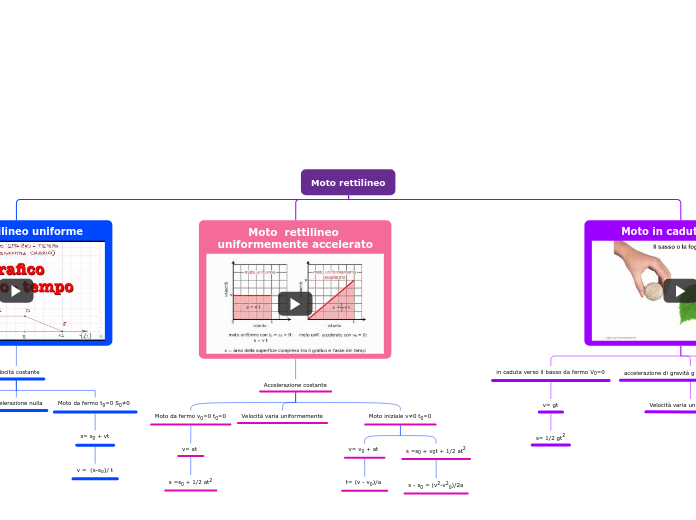
Stabilisce come varia la velocità di un pianeta lungo l'orbita. La seconda legge di Keplero definisce che:
Il raggio vettore che va dal Sole a un pianeta spezza aree uguali in intervallo di tempi uguali.
Infatti, se indichiamo la posizione del pianeta lungo l'orbita a intervalli di tempo regolari, vediamo che, allontanandosi dal perielio, il pianeta percorre archi via via più brevi.
Le superfici SPP' e SAA' sono spaz- zate in tempi uguali perché hanno la stessa area. Quindi il pianeta percorre in tempi uguali gli archi PP', più lungo, e AA', più breve. Allora la velocità del pianeta attorno al perielio è maggiore della velocità attorno all'afelio.
La terza legge di Keplero mette in relazione le distanze dei pianeti dal Sole con i tempi di percorrenza dell'orbita
più un pianeta è lontano dal sole, maggiore è il tempo che esso impiega per completare la propria orbita
Il rapporto tra il cubo del semiasse maggiore a dell'orbita e il quadrato del periodo di rivoluzione T è lo stesso per tutti i pianeti.
