Le disequazioni di primo grado sono separate non con il simbolo = ma con i simboli > per indicare "maggiore di"
< per indicare "minore di"
≥ per indicare "maggiore o uguale a"
≤ per indicare "minore o uguale a"
Una disequazione è una disuguaglianza in cui vengono confrontate due espressioni algebriche in una o più incognite.
Nelle disequazioni possiamo avere un primo e un secondo membro
Una disequazione si dice di primo grado quando compaiono incognite di potenza 1 Esempio: x + 2 < 7
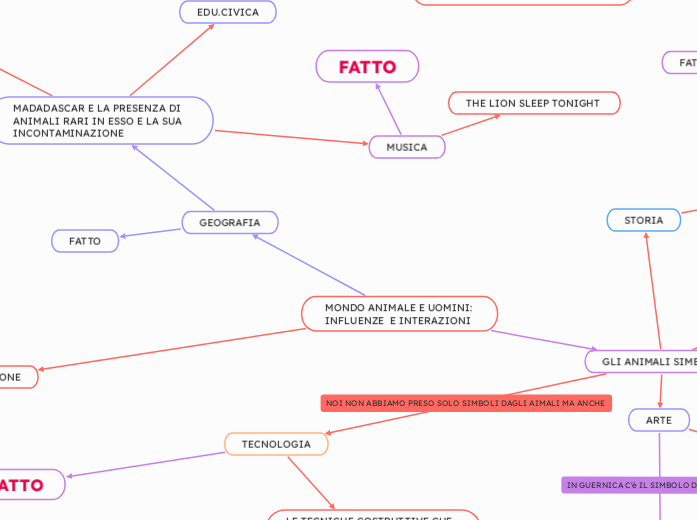
Soluzioni
Sempre verificata → qualsiasi valore sostituito all’incognita rende la disequazione vera
Impossibile → quando non esistono valori che rendano vera la disequazione
Determinata → l’incognita può essere sostituita dai valori compresi in un intervallo
LE DISEQUAZIONI
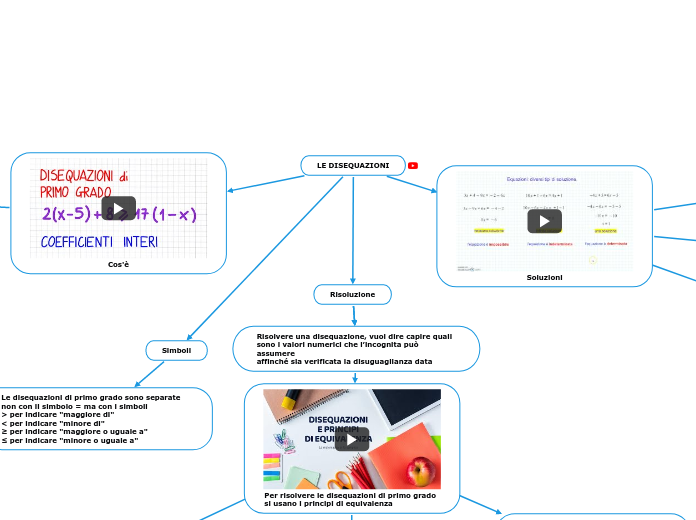
Cos'è
Simboli
Risoluzione
Risolvere una disequazione, vuol dire capire quali
sono i valori numerici che l’incognita può assumere
affinché sia verificata la disuguaglianza data
Per risolvere le disequazioni di primo grado si usano i principi di equivalenza
Primo principio di equivalenza: Sommando o sottraendo a entrambi i membri di una disequazione una stessa espressione algebrica intera, si ottiene una disequazione equivalente a quella data
Secondo principio di equivalenza delle disequazioni: Moltiplicando o dividendo entrambi i membri di una disequazione per uno stesso numero positivo, si ottiene una disequazione equivalente a quella data.
Terzo principio di equivalenza delle disequazioni: Moltiplicando o dividendo entrambi i membri di
una disequazione per uno stesso numero negativo e cambiando il verso del simbolo di
disuguaglianza, si ottiene una disequazione equivalente a quella data.