MAT.126
4.3
Riemann Sums and Definite Integrals
Evaluate a definite integral using limits
Evaluating Definite Integrals
Apply the limit definition.
Use geometric formulas if applicable.
Use other techniques (coming soon).
Theorem 4.5
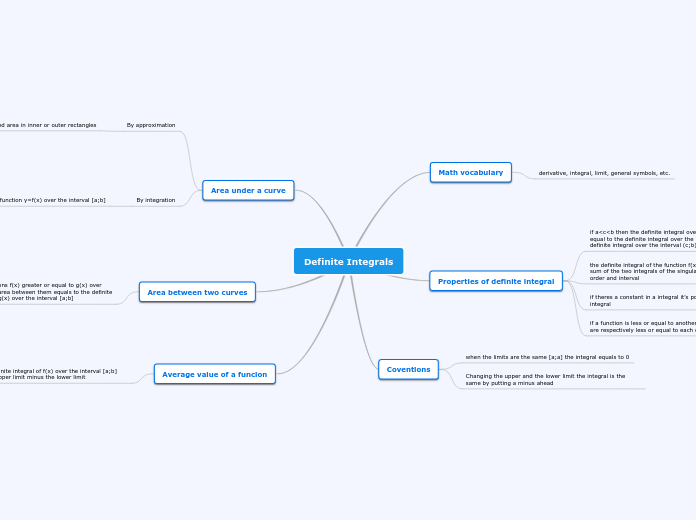
The Definite Integral as the Area of a Region
If f is continuous and nonnegative on the closed interval [a,b], then the area of the region bounded by the graph of f, the x-axis, and the vertical lines x=a and x=b is given by
Area = S_a^b f(x) dx.
Theorem 4.4
Continuity Implies Integrability
If a function f is continuous on the closed interval [a,b], the f is integrable on [a,b]. That is, S_a^b f(x) dx exists.
Definite vs. Indefinite Integrals
Indefinite integrals are families of functions.
Definite integrals are numbers.
Definition
If f is defined on the closed interval [a,b] and the limit of Riemann sums over partitions delta exists, then f is said to be integrable on [a,b] and the limit is denoted by
lim_{||delta||-->0} E_{i=1}^n f(c_i) delta x_i
= S_a^b f(x) dx.
The limit is called the definite integral of f from a to b. The number a is the lower limit of integration, and the number b is the upper limit of integration.
Evaluate a definite integral using properties of definite integrals
Theorem 4.8
Preservation of Inequality
If f is integrable and nonnegative on the closed interval [a,b], then
0 <= S_a^b f(x) dx.
If f and g are integrable on the closed interval [a,b] and f(x) <= g(x) for every x in [a,b], then
S_a^b f(x) dx <= S_a^b g(x) dx.
Theorem 4.7
Properties of Definite Integrals
If f and g are integrable on [a,b] and k is a constant, the functions kf and f +- g are integrable on [a,b], and
S_a^b kf(x) dx = k S_a^b f(x) dx
S_a^b [f(x) +- g(x)] dx
= S_a^b f(x) dx +- S_a^b g(x) dx
Theorem 4.6
Additive Interval Property
If f is integrable on the three closed intervals determined by a, b, and c, then
S_a^b f(x) dx
= S_a^c f(x) dx + S_c^b f(x) dx.
Definitions of Two Special Definite Integrals
If f is defined at x=a, then we define S_a^a f(x) dx = 0.If f is integrable on [a,b], then we define S_b^a f(x) dx = -S_a^b f(x) dx.Understand the definition of a Riemann sum
Norm
The width of the largest subinterval of a partition delta is the norm of the partition and is denoted by ||delta||.
A partition in which all of the subintervals are of equal width is regular.
Riemann Sum
Let f be defined on the closed interval [a,b], and let delta be a partition of [a,b] given by
a = x_0 < x_1 < x_2 < . . . < x_{n-1} < x_n = b
where delta x_i is the width of the ith subinterval. If c_i is any point in the ith subinterval [x_{i-1},x_i], then the sum
E_{i=1}^n f(c_i) delta x_i, x_{i-1} <= c_i <= x_i
is called a Riemann sum of f for the partition delta.
Intervals of unequal width
When taking a limit, it's the width of the largest subinterval that must go to zero.
Limits of sums
Area
Arc lengths
Average values
Centroids
Volumes
Work
Surface areas