MAT.126
5.5
Bases Other Than e and Applications
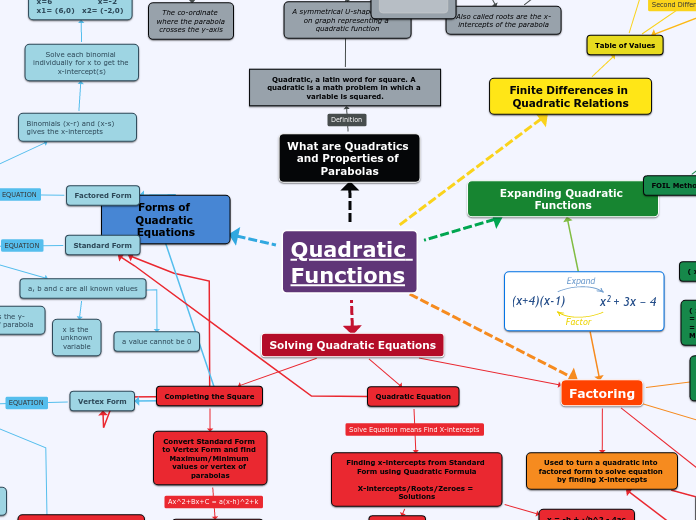
Differentiation and Integration
A comparison of 4 rules for differentiation
Constant Rule
d/dx[e^e] = 0
Power Rule
d/dx[x^e] = e x^{e-1}
Exponential Rule
d/dx[e^x] = e^x
Logarithmic differentiation
d/dx[x^x] = x^x (1 + ln x)
Integration
When confronted with an integral of the form
S a^x dx
there are two choices.
One is to convert the exponential expression with base a to an equivalent exponential expression with base e. That is, consider
S e^{(ln a)x} dx
remembering that ln a is a constant.
The second option is to use the following integration formula,
S a^x dx = (1/ln a) a^x + C
Derivatives for Bases Other Than e
Let a be a positive real number (a<>1) and let u be a differentiable function of x.
d
---[a^x] = (ln a) a^x dx
d du
---[a^u] = (ln a) a^u ---- dx dx
d 1
---[log_a x] = -------- dx (ln a) x
d 1 du
---[log_a u] = -------- --- dx (ln a) u dx
Applications of Exponential Functions
Logisitic Growth
Continuously Compounded Interest
Compound Interest
Bases Other than e
Common Logarithmic Function
The logarithm with base 10.
Inverse Function Properties
y = a^x if and only if x = log_a ya^{log_a x} = x, for x > 0log_a a^x = x, for all xLogarithmic Properties
log_a 1 = 0log_a xy = log_a x + log_a ylog_a x/y = log_a x - log_a ylog_a x^n = n log_a xDefinition of Logarithmic Function to Base a
If a is a positive real number (a<>1) and x is any positive real number, then the logarithmic function to the base a is denoted by log_a x and is defined as
log_a x = (1/ln a) ln x
Laws of Exponents
a^0 = 1a^x a^y = a^{x+y}a^x / a^y = a^{x-y}(a^x)^y = a^{xy}Definition of Exponential Function to Base a
If a is a positive real number (a<>1) and x is any real number, then the exponential function to the base a is denoted by a^x and is defined by
a^x = e^{(ln a)x}
If a=1, then y=1^x=1 is a constant function.