MPM2D1
.
Quadratic Systems
Perfect Square Trinomial:
- square first term (a2)
- multiply a and b by 2 (2ab)
- square last term
(a+b)2 = a2 +2ab+b2
Difference of Squares:
- square first term (a2)
- square last term (b2)
must be two identical equations with opposite values: (a+b) (a-b)
Removing a common factor:
Finding the GCF divisible by all numbers.
ex. 6x2 + 12x
=6x(x+20)
Solution to #2:
Find GCF which is 5 than divide all numbers by it.
5x2-10x+5
=5(x2-2x+1) now that it is in simple trinomial form we can solve it using the simple trinomial method.
P: 1
S:-2 two numbers :-1,-1
5(x-1) (x-1)
decomposition/ grouping:
ex. 2x+4x+3x+6
P: 2 x 6=12 S:7 > 4,3
(2x+4x) + (3x+6)
2x (x+2) + 3(x+2) --> (x+2) is the GCF
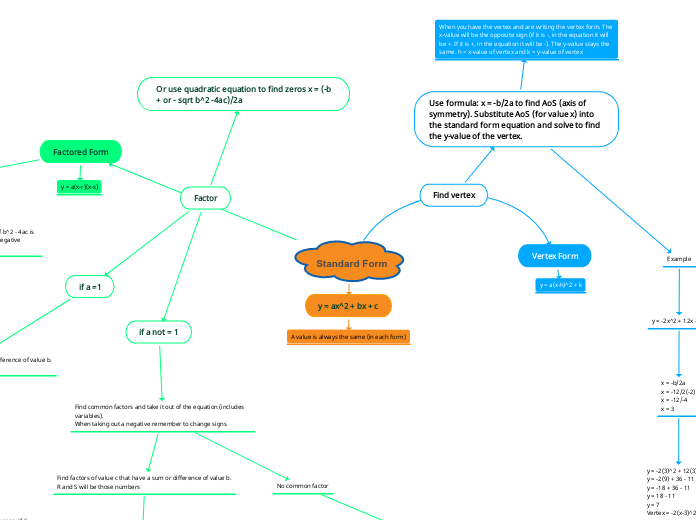
Standard form: y = ax2+ bx + c
Vertex form: y + a (x-h)2+ k
Factored form: y = a (x-r) (x-s)
#2: Simplify the following expressions 5x2-10x+5.
Distributive property:
Also known as FOIL
F - multiply first terms
O - multiply outside terms
I - multiple inside terms
L - multiple last terms
Solution to #1:
R= (400+20x) (300-10x)
O= (400+20x) (300-10x)
x=-20,30
$: 400+20(30)= 400+600= $1000
maximum area: find vertex
area= x(400-2x)
400=2x
200=x
x- value of vertex:100
y-value of vertex: a=100(400-2(100))=20,000
Therefore max area would be 20,000m2 with dimensions of 100m x 200m.
#1: A theatre company has 300 season ticket subscribers. The board of directors has decided to raise the price of a season ticket from the current price of $400. A survey of the subscribers has determined that, for every $20 increase in price, 10 subscribers would not renew their season tickets.
a)Write an algebraic model to represent the theatre's total season ticket sales revenue.
b)At what price will the maximum revenue occur? How many subscribers will the theatre have when the maximum revenue occurs?
Trigonometry
non right triangle
The sine law:
Missing Angles :
sin a/A = sin b/B = sin c/C
Missing Sides:
a/sinA = b/sinB =c/sinC
The cosine law:
a2 = b2 +c2 - 2bc Cos A
b2 = a2+c2 - 2ac Cos B
c2 = a2 +b2 - 2ab Cos C
right triangle:
Pythagorean theorem:
Hypoteneuse2 = Opposite2 + Adajcent2
solution to #1:
sin= 59.7/330.7
sin-1(59.7/330.7)
=10.40040843
=10.4 degrees
therefore the angle of elevation of the escalator is 10.4 degrees
Solution for #2:
cosine law:
SOHCAHTOA:
SOH - Sin, Opposite, Hypotenuse
CAH - Cos, Adjacent, Hypotenuse
TOA - Tan, Opposite, Adjacent
#1: The world’s longest escalator is in the subway system in St. Petersburg, Russia. The escalator is 330.7 meters long and rises a vertical distance of 59.7 meters. What is the angle of elevation of the escalator? Round to the nearest tenth of a degree.
#2: Cara is standing in the centre of a field. From where she is standing, she can see
four posts at different positions on the field, as shown in the diagram. How far apart
are posts A and B, to the nearest tenth of a meter?
Analytic Geometry
Slope: the slope formula is used when a question requires y=mx+b format to solve the problem such as right bisector and altitude questions.
MAB= Y2-Y1
_____
X2-X1
#1: Determine midpoint of A(9,3) and B (3,5).
Soloution to #1:
put coordinates into midpoint formula.
m= (9+3, 3+5) divided by 2
m=(12, 8)
m= (6, 4)
Length formula: Is used when trying to find the difference between two line segments.
L = square root (X2 - X1)
+ (Y2-Y1)
Midpoint formula:
The midpoint formula is used for finding the midpoint between two line segments coordinates.
m=(X1+X2 , Y1+Y2) divided by 2
#2: A helicopter has crashed at point P (-1,3) the nearest hospital is at x+y-5 =0. Find the shortest distance from point P(-1, 3) to the line x + y – 5 = 0, round to nearest tenth.
Solution to #2:
eq. of the perpendicular line m=-1 so m=1
y=mx+b --> 3+1(-1)+b
3=-1+b
4=b ---> y=x+4
So now to find POI
y=-x+5 = y=x+4
-x+5=x+4
=x+x
1/2=2x/2
1=x
now sub x=1 into y=x+4
y+1/2+8/2
POI: (1/2,9/2)
to find length sub into length formula:
(1/2-1)2 (9/2-3)2
=square root of 3/22 3/22
= 0.8660254038
=0.9, 0.9
Quadratic Formula:
x= -b+ square root of b2-4ac divided by 2(a)
Linear Systems
#1:
Phoenix health club charges $200 initiation fee and $15 per a month.
Champion health club charges $100 initiation fee and $20 per a month. Solve the linear system using the method of substitution. Which company would be more expensive for a year?
Solution to #1:
Let m represent number of months
Let c represent cost
c= 200 +15m (1) c=100+20m (2)
sub (1) into (2)
200+15m = 100+20m
200 - 100 + 20m - 15m
100=5m divide both sides by 5, therefore m=20
sub m=20 into (1)
c= 200 +15(20)
200+300=500 therefore POI (20,500)
Part 2:
c=200+15(12) = 380
c=100+20(12) = 340
Therefore the more inexpensive option is the Champion club by $40 less.
Solution to #2:
Label equations with 1,2
4x + 3y =20 (1)
2x - 3y +40 (2)
For these two equations we will use addition since the variable holding the same value of the coefficient 3y has opposite values (+ -). Therefore adding them cancels each other out.
6x=60 divide both sides by 6
x = 10
Sub x=10 into an equation to find y value
#2: Solve the system by elimination.
4x + 3y = 20
2x - 3y =40
In the method of substitution we sub one equation into another to find our missing x or y value.
ex. y=2x-3 (1) x+y=6 (2) sub (1) into (2) x+2x-3=6 3x-3=6+3 3x=9 x=3
Substitution
Elimination
The method of elimination can be used for adding, subtracting or multiplying to eliminate x or y to find POI/ x and y values.
Graphing
ex. y=mx+b --->
blue is the slope and green is the y-int
When using the graphing method, you use your y-intercept to start and your slope to do rise/run.