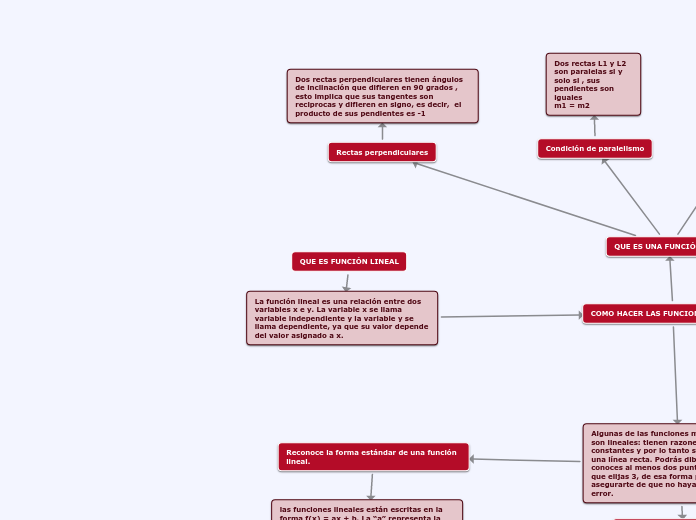
QUE ES FUNCIÓN LINEAL
La función lineal es una relación entre dos variables x e y. La variable x se llama variable independiente y la variable y se llama dependiente, ya que su valor depende del valor asignado a x.
COMO HACER LAS FUNCIONES LINEALES?
QUE ES UNA FUNCIÓN AFÍN
Rectas perpendiculares
Dos rectas perpendiculares tienen ángulos de inclinación que difieren en 90 grados , esto implica que sus tangentes son reciprocas y difieren en signo, es decir, el producto de sus pendientes es -1
Condición de paralelismo
Dos rectas L1 y L2 son paralelas si y solo si , sus pendientes son iguales
m1 = m2
Rectas paralelas
Dos rectas paralelas tienen el mismo ángulo de inclinación, esto implica que sus tangentes son iguales, es decir, las pendientes coinciden.
es una función cuya gráfica es una línea recta, por lo que también se le denomina función lineal.
Esta función se puede escribir de la siguiente forma: f(x) = mx + b, donde m y b son números reales tales que, m se llama pendiente y b es el punto de corte con el eje de las ordenadas.
Si m es mayor que cero (m>0), se dice que la recta es creciente.
Si m es menor que cero (m<0), se dice que la recta es decreciente.
Si b = 0, la recta pasa por el origen.
Algunas de las funciones más importantes son lineales: tienen razones de cambio constantes y por lo tanto se grafican con una línea recta. Podrás dibujar la línea si conoces al menos dos puntos, pero es mejor que elijas 3, de esa forma podrás asegurarte de que no hayas cometido un error.
Conecta los puntos.
Para 2 puntos cualesquiera, solo hay una forma de conectarlos con una línea recta. Utiliza una regla para unirlos con una línea. Debes notar que si graficas 3 puntos y no todos caen en la misma línea, has cometido algún error. Regresa y calcula todo de nuevo.c
Dibuja los puntos
coloca los puntos en el sistema de coordenadas utilizando los valores que obtuviste al resolver las 3 ecuaciones.
Busca por lo menos dos puntos.
El gráfico tendrá una línea recta porque tienes una función lineal, por lo tanto, realmente solo necesitas dos puntos. En general, sin embargo, debes encontrar 3 puntos en lugar de 2 para revisar la precisión.
Reconoce la forma estándar de una función lineal.
las funciones lineales están escritas en la forma f(x) = ax + b. La “a” representa la gradiente de la recta, lo cual da la razón de cambio de la variable dependiente. A esto se le conoce como la “pendiente”. La “b” representa el intercepto con el eje Y. Este es el valor de la variable dependiente o en otras palabras, el valor de la función cuando X = 0.