av Wafiqah Wahab för 4 årar sedan
317
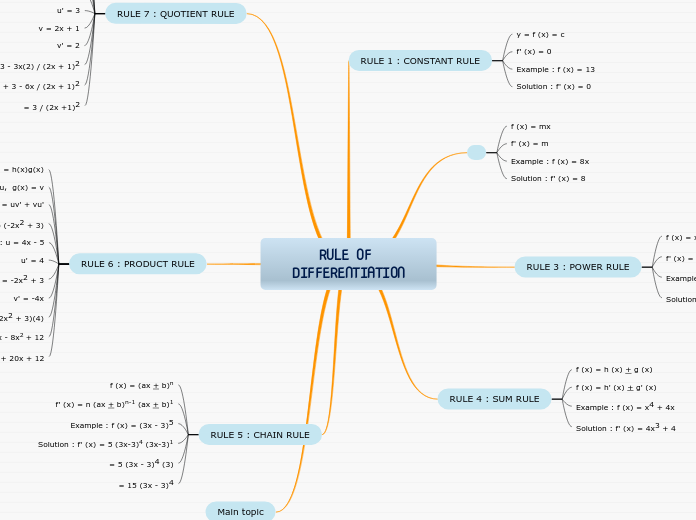
RULE OF DIFFERENTIATION
Understanding the rules of differentiation is essential for solving various mathematical problems, especially in calculus. Differentiation rules include several key principles: the product rule, chain rule, sum rule, quotient rule, constant rule, and power rule.