The Different Types Of Probability
2. Choosing a marble from a bag
- Probability of choosing a certain color marble given that another marble has already been chos
en.
background
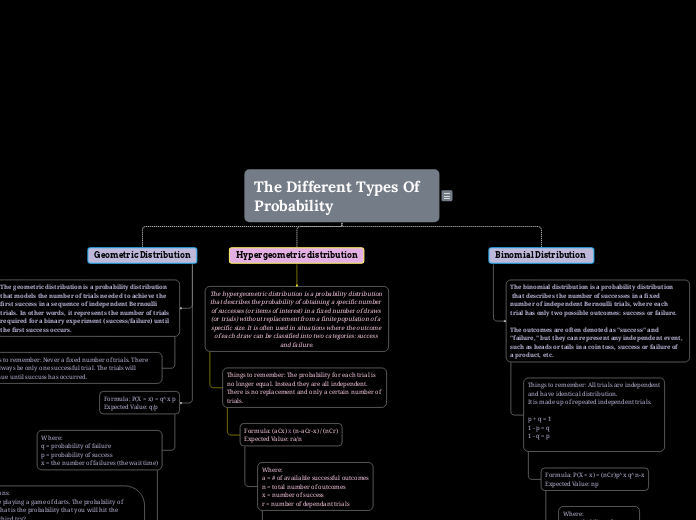
Binomial Distribution
The binomial distribution is a probability distribution
that describes the number of successes in a fixed
number of independent Bernoulli trials, where each
trial has only two possible outcomes: success or failure.
The outcomes are often denoted as "success" and "failure," but they can represent any independent event, such as heads or tails in a coin toss, success or failure of
a product, etc.
Things to remember: All trials are independent
and have identical distribution.
It is made up of repeated independent trials.
p + q = 1
1 - p = q
1 - q = p
Formula: P(X = x) = (nCr)p^x q^n-x
Expected Value: np
Where:
p = probability of success
q = probability of failure
x = number of successes
n = total number of trials
Example Questions:
Find the probability of getting at least 5 times head-on tossing an unbiased coin for 6 times?
On average, every one out of 10 telephones is found busy. Six telephone numbers are selected at random. Find the probability that four of them will be busy.
Hypergeometric distribution
The hypergeometric distribution is a probability distribution that describes the probability of obtaining a specific number of successes (or items of interest) in a fixed number of draws (or trials) without replacement from a finite population of a specific size. It is often used in situations where the outcome of each draw can be classified into two categories: success and failure.
Things to remember: The probability for each trial is
no longer equal. Instead they are all independent.
There is no replacement and only a certain number of
trials.
Formula: (aCx) x (n-aCr-x) / (nCr)
Expected Value: ra/n
Where:
a = # of available successful outcomes
n = total number of outcomes
x = number of success
r = number of dependant trials
Example Questions:
A deck of cards contains 20 cards: 6 red cards and 14 black cards. 5 cards are drawn randomly without replacement. What is the probability that exactly 4 red cards are drawn?
In a small pond there are 50 fish, 10 of which have been tagged. A fisherman's catch consists of 7 fish (assume his catch is a random selection done without replacement). What is the probability that exactly 2 tagged fish are caught?
Geometric Distribution
Formula: P(X = x) = q^x p
Expected Value: q/p
Where:
q = probability of failure
p = probability of success
x = the number of failures (the wait time)
Example Questions:
Suppose you are playing a game of darts. The probability of success is 0.4. What is the probability that you will hit the bullseye on the third try?
Suppose Max owns a lightbulb manufacturing company and determines that 3 out of every 75 bulbs are defective. What is the probability that Max will find the first faulty lightbulb on the 6th one that he tested?
The geometric distribution is a probability distribution that models the number of trials needed to achieve the first success in a sequence of independent Bernoulli trials. In other words, it represents the number of trials required for a binary experiment (success/failure) until the first success occurs.
Things to remember: Never a fixed number of trials. There will always be only one successful trial. The trials will continue until succuss has occurred.