av Jennifer Lewis för 4 årar sedan
717
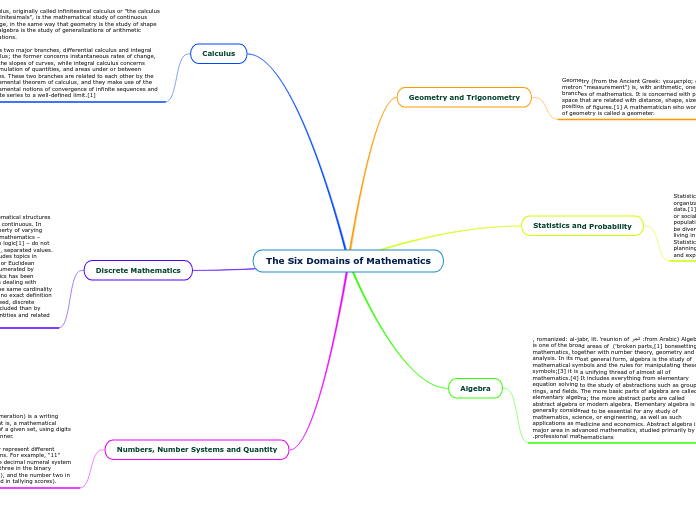
The Six Domains of Mathematics
Statistics is a field focused on the collection, analysis, interpretation, and presentation of data, and begins with defining a statistical population or model. This can involve diverse groups like all people in a country or every atom in a crystal, covering aspects from data collection planning to the design of surveys and experiments.