av Joel Lisboa för 2 årar sedan
581
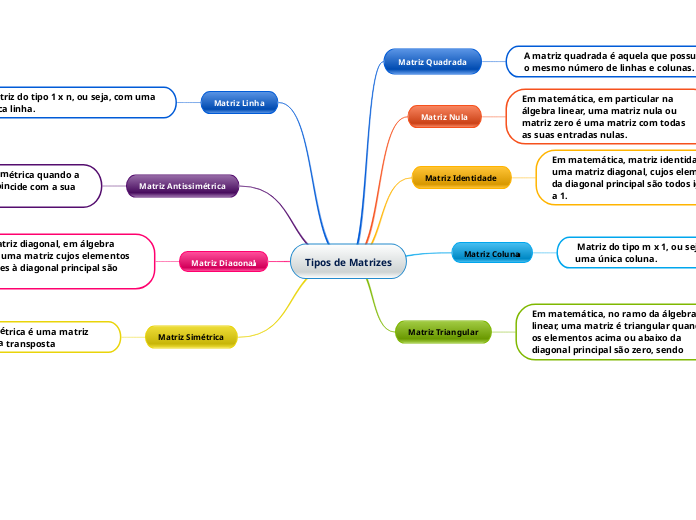
Tipos de Matrizes
As matrizes são estruturas fundamentais em álgebra linear, utilizadas para representar e manipular dados em diversas aplicações matemáticas. Elas podem ser classificadas em vários tipos, como matrizes quadradas que possuem igual número de linhas e colunas, matrizes colunas que possuem apenas uma coluna, e matrizes linha que possuem apenas uma linha.