av Emily Wheeler för 12 månader sedan
141
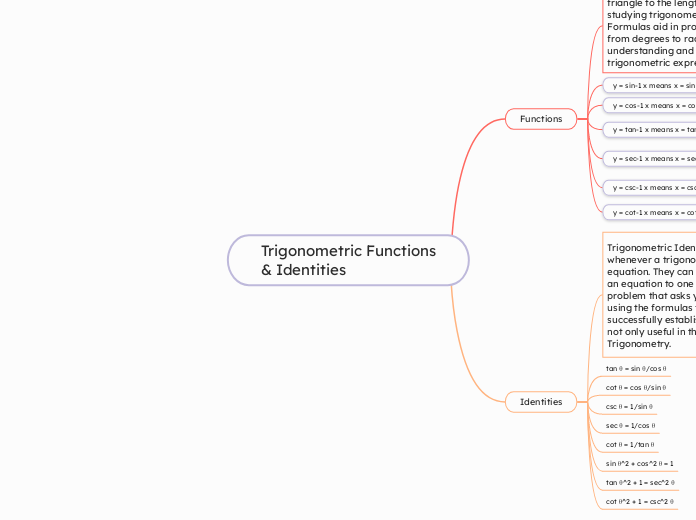
Trigonometric Functions & Identities
Trigonometric identities are essential tools in mathematics, particularly in the study of trigonometry, as they help simplify and solve equations involving trigonometric functions. These identities allow for the transformation of expressions into more manageable forms, which is crucial for proving relationships and solving problems.