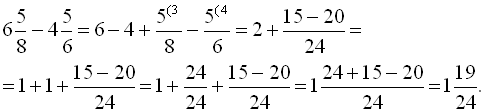Дроби
Звичайний дріб або простий дріб — запис раціонального числа в вигляді відношення двох чисел. Ділене m називається чисельником дробу, а дільник n — знаменником дробу.
Правильним дробом називається дріб, у якого чисельник менше знаменника. Неправильним дробом називається дріб, у якого чисельник більший або рівний знаменнику.
Будь-який неправильний дріб можна представити в вигляді натурального числа або суми натурального числа і правильного дробу.
Мішаним числом називається число, яке записано в вигляді цілого числа і правильного дробу і розуміється, як сума цього числа і дробу.
Дроби в нашому житті
Люди постійно використовують дроби в повсякденному житті, але просто не задумуються про це. Ми користуємось дробами коли знаходимось в лікарні, на кухні, під час будівництва, в музиці, архітектурі та багато іншого.
Планета Земля
Земля і дроби.
- 3/4 – покрито водою
- 1/4 – суша
- 1/8 – поверхня Землі на якій можна жити
- 1/8 - пустелі, гори, ліси,
- 3/32 – місця , де можуть жити люди
- 1/32 – поля, де вирощують врожай.
Уявіть собі, що яблуко – це наша Земля . Розріжте його на частинки і ви побачите, яка мала частина Землі придатна для життя людини.
Людина
Сон 1/3
Навчання 1/4
Виконання домашньої роботи 1/12
Прогулянки 1/8
Споживання їжі 1/48
Музика
Музика немислима без нот, кожна з яких має свою тривалість. Рахуючи тривалість нот « раз - і - два – і – три - і - …», називаємо початок натурального ряду чисел. А такі назви тривалості нот, як «половина, четвертина, восьма, шістнадцята і т.д.» зображаються дробами.
Дії над десятковими дробами
Округлення десяткових дробів
При округленні десяткових дробів користуються одним із таких двох правил.
Правило 1
Щоб округлити десятковий дріб до певного розряду дробової частини (до певного десяткового знака), треба:
1) відкинути всі десяткові знаки, які стоять після цього розряду;
2) якщо перша з відкинутих цифр була 5, 6, 7, 8 або 9, то останню залишену цифру збільшити на одиницю;
3) якщо перша з відкинутих цифр була 0, 1, 2, 3 або 4, то останню залишену цифру записати без змін.
Правило 2
Щоб округлити десятковий дріб до певного розряду цілої частини вищого розряду одиниць, треба: відкинути всі цифри дробової частини (всі десяткові знаки); цілу частину округлюємо за правилом округлення натуральних чисел.
ділення десяткових дробів
Ділення десяткового дробу на натуральне число виконується так само, як ділення натурального числа на натуральне, але кому в частці ставлять після того, як закінчено ділення цілої частини.
Розглянемо тепер ділення десяткового дробу на десятковий дріб. Нехай треба поділити 8,316 на 2,31. Для цього і в діленому, і в дільнику перенесемо кому вправо на стільки цифр, стільки їх є після коми в дільнику (в даному прикладі на дві). Іншими словами, помножимо ділене і дільник на 100 – від цього частка не зміниться. Тоді треба поділити дріб 831,6 на натуральне число 231, тобто задача зводиться до вже знайомого випадку.
Щоб поділити десятковий дріб на 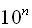 , треба в цьому дробі перенести кому на п цифр вліво (при цьому у випадку необхідності зліва приписати потрібне число нулів).
, треба в цьому дробі перенести кому на п цифр вліво (при цьому у випадку необхідності зліва приписати потрібне число нулів).
Як для натуральних чисел ділення не завжди можна виконати, так його не завжди можна виконати й для десяткових дробів.
Може виявитися, що одні числа записані у вигляді звичайних дробів, інші – у вигляді мішаних дробів, треті – у вигляді десяткових дробів. Виконувати дії над такими числами можна по-різному: перетворити десяткові дроби в звичайні і користуватись правилами дій над звичайними дробами або перетворити звичайні і мішані дроби в десяткові дроби (якщо це можливо) і застосувати правила дій над десятковими дробами.
множення дробів
Щоб помножити один десятковий дріб на інший, потрібно виконати множення, не звертаючи уваги на коми, і в отриманому добутку відокремити праворуч комою стільки цифр, скільки їх стоїть після коми в обох множниках разом. Наприклад, 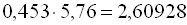 .
.
Щоб помножити десятковий дріб на 10, 100, 1000 і т.д., необхідно в цьому дробі перенести кому вправо на стільки цифр, скільки нулів у множника (дописавши у випадку необхідності до дробу праворуч певне число нулів). Наприклад: 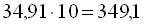 ;
;  .
.
додавання та віднімання
При додаванні (відніманні) десяткових дробів числа записують так, щоб однакові розряди були записані один під одним, а кома – під комою, і додають (віднімають) як натуральні числа
Складові дробу
Чисельник дробу — число, яке записане над рискою дробу.
Знаменник дробу — число, яке записане під рискою дробу.
Знаменник дробу показує на скільки рівних частин поділили щось ціле. А чисельник дробу показує скільки таких частин взяли
Знаменник
А число чи вираз під рискою, це знаменник.
Оскільки дріб — це позначення операції ділення, то:
чисельник є діленим
знаменник є дільником
Риска дробу
Риска дробу- риска, яка заміняє дію ділення чисельника на знаменник.
Чисельник
Чисельник- число, або алгебраїчний вираз що стоїть над рискою дробу
Дії над звичайними дробами
Із дробами можна виконувати звичайні арифметичні операції: додавання, множення, віднімання, ділення. Але потрібно дотримуватись правил для виконання кожної з дій.
ділення
При діленні дробу на дріб чисельник діленого множать на знаменник дільника, а знаменник діленого – на чисельник дільника. Перший добуток служить чисельником, а другий – знаменником частки: 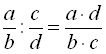 . Наприклад,
. Наприклад,  .
.
Якщо потрібно поділити дріб на дріб, у випадку коли один чи обидва дроби – мішані, то потрібно попередньо зобразити мішаний дріб у вигляді неправильного дробу.
Будь-яку ціле число можна зобразити у вигляді дробу. Наприклад, 
 ,
, 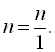
Два числа називаються взаємно оберненими, якщо їх добуток дорівнює 1. Наприклад, 5 і  , х і
, х і 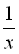
множення
Множення звичайних дробів виконується таким чином:  , тобто перемножують окремо чисельники, окремо знаменники. Перший добуток роблять чисельником, другий – знаменником. Отриманий дріб, якщо це можливо, скорочують.
, тобто перемножують окремо чисельники, окремо знаменники. Перший добуток роблять чисельником, другий – знаменником. Отриманий дріб, якщо це можливо, скорочують.
При множенні мішаних дробів їх попередньо зображають у вигляді неправильних дробів, а потім перемножують. Наприклад, 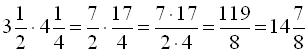 .
.
додавання/ віднімання
При додаванні (відніманні) дробів з однаковими знаменниками до чисельника першого дробу додають чисельник другого дробу (від чисельника першого дробу віднімають чисельник другого дробу) і залишають той же знаменник. Отриманий дріб, якщо це можливо, скорочують. Наприклад,  ,
,  .
.
При додаванні (відніманні) дробів з різними знаменниками переважніше попередньо звести їх до найменшого спільного знаменника. Наприклад, 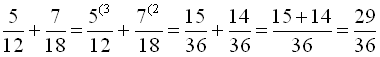 .
.
При додаванні мішаних дробів потрібно додати окремо цілі частини і дробові частини. Наприклад,
 .
.
При відніманні мішаних дробів варто розрізняти такі випадки:
a) дробова частина зменшуваного більше або дорівнює дробовій частині від’ємника; у цьому випадку від цілої частини зменшуваного віднімають цілу частину від’ємника, а від дробової частини зменшуваного – дробову частину від’ємника. Наприклад, 
b) дробова частина зменшуваного менше дробової частини від’ємника; в цьому випадку одну з одиниць цілої частини зменшуваного потрібно замінити таким дробом, який їй дорівнює. Наприклад, 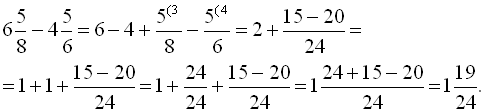
Види дробів
Всі математичні дроби діляться на два великих розряди:
- звичайні
- десяткові;
Звичайним дробом називається вираз a/b, де a є N і b є N. Приклади звичайних дробів: 2/5; 4/10;
Звичайні дроби (і мішані числа), знаменниками яких є числа 10, 100, 1000 і т.д., називаються десятковими. Приклади десяткових дробів:
0,2; 21,90; 5,01
мішані
Будь-який неправильний дріб можна представити в вигляді натурального числа або суми натурального числа і правильного дробу.
Мішаним числом називається число, яке записано в вигляді цілого числа і правильного дробу і розуміється, як сума цього числа и дробу.
звичайні (правильні, неправильні)
Звичайний дріб записується як співвідношення, в якому в чисельнику відображається, скільки взято частин від числа, а знаменник показує, на скільки частин розділена одиниця. Якщо в дробу чисельник менше знаменника, то перед нами правильний дріб. Наприклад: ½, 3/5, 8/9.
Якщо чисельник дорівнює знаменника або більше його, то ми маємо справу з неправильним дробом. Наприклад: 5/5, 9/4, 5/2 При розподілі чисельника на знаменник може вийти кінцеве число. Наприклад, 40/8 = 5. Отже, будь-яке ціле число може бути записано у вигляді звичайної неправильного дробу або ряду таких дробів.
десяткові
Будь-яке число, знаменник дробової частини якого виражається одиницею з одним або декількома нулями, можна представити у вигляді десяткового дробу.
Якщо дріб правильний, тоді перед комою пишуть цифру 0.
Наприклад, замість 21/100 пишуть 0,21 (читають: «0 цілих і 21 сота»).
Після коми чисельник дробової частини повинен мати стільки ж цифр, скільки нулів в знаменнику.
Завдання
Історія
Вперше оперувати дробами почали на території Єгипту і Вавилона. Підхід математиків двох держав мав значні відмінності. Однак початок і там і там було покладено однаково. Першою дробом стала половина або 1/2. Далі виникла чверть, третина і так далі. Згідно з даними археологічних розкопок, історія виникнення дробів налічує близько 5 тисяч років. Вперше частки числа зустрічаються в єгипетських папірусах, і на вавілонських глиняних табличках.
дроби в Стародавній Русі
На руській землі першим математиком, який виклав розподіл цілого на частини, став новгородський монах Кирик.

У 1136 році він написав працю, в якій виклав метод «числення років». Кирик займався питаннями хронології і календаря. У своїй праці він привів в тому числі і розподіл години на частини: п`яті, двадцять п`яту і так далі частки. Розподіл цілого на частини застосовувалося при розрахунку розміру податку в XV-XVII століттях. Використовувалися операції додавання, віднімання, ділення і множення з дробовими частинами.
Саме слово «дріб» з`явилося на Русі в VIII столітті. Воно походить від дієслова «дробити, розділяти на частини». Для назви дробів наші предки використовували спеціальні слова. Наприклад, 1/2 позначалася як половина або полтина, 1/4 - четь, 1/8 - полчеть, 1/16 - полполчеть і так далі. Повна теорія дробів, мало чим відрізняється від сучасної, була викладена в першому підручнику з арифметики, написаному в 1701 році Леонтієм Пилиповичем Магницким. «Арифметика» складалася з декількох частин. Про дроби докладно автор розповідає в розділі «Про числах ламаних або з частками». Магницкий наводить операції з «ламаними» числами, різні їх позначення.
дроби в Римській імперії
Римська система дробів була пов'язана з мірою ваги, званої «асс». Вона ділилася на 12 часток. 1/12 асса називалася унцією. Для позначення дробів існувало 18 назв. Наведемо деякі з них:
семис — половина асса;
секстанте — шоста частка асса;
семиунция — пів-унції або 1/24 асса.
Незручність такої системи полягала в неможливості подати число у вигляді дробу зі знаменником 10 або 100. Римські математики подолали труднощі з допомогою використання відсотків.
дроби в Єгипті
Види звичайних дробів сьогодні включають в себе і так звані єгипетські. Вони являють собою суму кількох доданків виду 1/n. Чисельник — завжди одиниця, а знаменник — натуральне число. З'явилися такі дроби, як не важко здогадатися, у стародавньому Єгипті. При розрахунках усі частки намагалися записувати у вигляді таких сум (наприклад, 1/2 + 1/4 + 1/8). Окремими позначеннями володіли тільки дробу 2/3 та 3/4 інші розбивалися на складові. Існували спеціальні таблиці, в яких частки числа представлялися у вигляді суми. Найдавніша з відомих згадок такої системи зустрічається у Математичному папірусі Рінда, датованому початком другого тисячоліття до нашої ери. Він включає таблицю дробів і математичні задачі з рішеннями і відповідями, поданими у вигляді сум дробів. Єгиптяни вміли складати, ділити і множити частки числа. Дробу в долині Нілу записувалися за допомогою ієрогліфів. Подання частки числа у вигляді суми доданків виду 1/n, характерну для стародавнього Єгипту, використовувалося математиками не тільки цієї країни. Аж до Середніх століть єгипетські дробу застосовувалися на території Греції та інших держав.

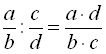 . Наприклад,
. Наприклад,  .
.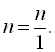
 , тобто перемножують окремо чисельники, окремо знаменники. Перший добуток роблять чисельником, другий – знаменником. Отриманий дріб, якщо це можливо, скорочують.
, тобто перемножують окремо чисельники, окремо знаменники. Перший добуток роблять чисельником, другий – знаменником. Отриманий дріб, якщо це можливо, скорочують.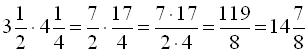 .
. ,
,  .
.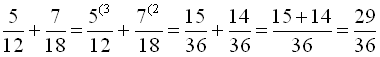 .
. .
.