It is very important that students are presented visual models as well as symbolic procedures so that they are able to link these connections to more advanced learning in later years.
I find visual representations are very helpful in grasping these concepts. Thanks Jovana!
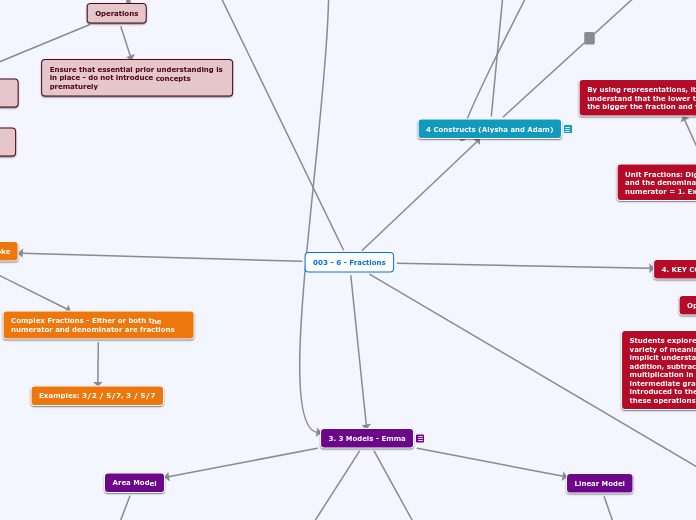
003 - 6 - Fractions
Fractions Across Strands and Grades - Tara
Teachers have identified the positive impacts of teaching fractions throughout the whole school year, rather than in one distinct unit. This is called punctuated, or chunked learning. Punctuated instruction allows for teachers to be to responsive to students' thinking and responses while working with fractions. This type of instruction also gives students the opportunity to connect fractions to other mathematical strands/concepts and begin to see the relationship between various math units rather than isolating concepts into distinct units/strands. Teachers who use this type of instruction with the teaching of fractions tend to narrow their instruction to key fraction concepts, which allows students to master the basic concepts and spend the time needed to deeply explore such concepts.
It is also stressed how critical it is that Teachers have a deep understanding of all of the main concepts of not only fractions, but of the main ideas of each math strand in the specific grade they are teaching. This allows Teachers to have a greater ability to connect main concepts from various strands, giving students a holistic educational experience.
The article also shared many great resources for teachers who may be struggling or may just want to learn some new instructional strategies for teaching fractions. One resource I found extremely useful was LearnTeachLead.ca/paying_attention_fractions. This document explores four documents to support Teachers, but 'Fractions Across the Stands and Grades: Simple Tasks' was very effective in my eyes.
1. Types of Fractions - Brooke
Complex Fractions - Either or both the numerator and denominator are fractions
Examples: 3/2 / 5/7, 3 / 5/7
Simple Fractions - Digits in both the numerator and denominator are integors
Improper Fractions - Numerator > Denominator
Examples: 3/2, 125/28
Mixed Fractions - A quantity represented by an integer and a proper fraction
Examples: 3 4/5, 12 1/29
Unit Fractions - Numerator = 1
Examples: 1/15, 1/29
Proper Fractions - Numerator < Denominator
Examples: 1/2, 21/26
4. KEY CONCEPTS JOVANA
Hi Jovana,
I think your subtopic related strongly to mine. I researched and summarized 'Fractions Across the Strands' and I read that it is important for Teachers to have a good foundational understanding of the main concepts of fractions in order to teach students properly and appropriately. I think having the knowledge about the main concepts of fractions not only makes you a better Teacher, but also makes you feel more competent in your ability to teach mathematical concepts.
Great ideas! Tara.
Students explore fraction concepts in a variety of meaningful ways, they develop an implicit understanding of the operations of addition, subtraction, division and multiplication in primary grades and in the intermediate grades, students are typically introduced to the formal algorithms for these operations.
Comparing and Ordering
Using Unit Fractions
When students are ordering fractions like 10/11 and 12/13, they can use the notion that the gap between the numerator and denominator is 1 fractional unit in both. They might further reason that since thirteenths are smaller than elevenths, there is less missing from the whole partitioned into thirteenths, so 12/13 is closer to 1 and therefore is greater than 10/11.
Using Common Numerators: when the numberator is the same, students can compare denominators to determine which one is smaller and larger.
Using Equivalent Fractions
Convert fractions to have the same numerator to be able to judge which fraction is bigger or smaller.
Using Benchmarks: A benchmark is a number or measurement that is internalized
and used to help judge other numbers or measurements
Example: “I know that 3 is less than half of 7, so 3/7 < 1/2. I also know that 5 is more than half of 9, so 5/9 > 1/2 . I know then that 5/9 > 3/7 .”
Constructing Models
There are many effective strategies for comparing and ordering fractions beyond determining a common
fractional unit, or common denominator
When students have a strong understanding of fractions they are able to use number
sense and proportional reasoning to make comparisons.
Equivalency: students are identifying different fractional units that can be used to describe a quantity (e.g., 1/3 =5/15 = 7/21).
Using manipulatives and models rather than algorithms is very useful in having students truly understand different methods of demonstrating the same quantity.
Using a Set Model to Represent Equivalent Fractions
4/6
However, although it is true that 4/6= 8/12 numerically, this shows an equivalent ratio rather than an equivalent fraction, since the whole has been changed from 6 to 12.
Using a Number Line Model to Represent Equivalent Fractions
The Whole: A fraction is partion of a whole.
It is helpful for students to recognize the various possibilities and to be flexible in the interpretation of fractions, that's why it is important to use concise language (e.g., part-whole, part-part, quotient and operator).
Unit Fractions: Digits in both the numerator and the denominator are integers; the numerator = 1. Example: 1/2, 1/7, 1/27.
By using representations, it helps students understand that the lower the denominator the bigger the fraction and vice versa.
3. 3 Models - Emma
Hi Emma,
As a visual learner myself I really like the options of different models to represent the fractions. Most of these models are ones that I forgot about so I am happy to be reminded of them. I think it is a great idea to share each of these models with students so they can in turn work with whichever model helps them to understand fractions the best!
-Brooke
Volume Model
In a volume model, a three-dimensional figure represents the whole. The whole is divided into fractional regions that are occupied by space within the figure.
Linear Model
The linear model is represented through a number line.
Holly - I particularly think that using a set model is helpful when learning fractions. I think this model is really useful for people who have a visual learning style to understand how fractions work. In the document, they use an example of 3 groups of fruit. It is easy to look at the picture and identify that one-third (1/3) of the fruit are pears. I think the set model closely relates to the "representation" aspect of the C.R.A. In addition, the set model makes me think of the coding activity we did yesterday where we saw the fractions represented with the coloured balls on the screen.
In a set model, a collection of items represents the whole amount. Subsets of the whole make up the fractional parts. A variety of materials can serve as set models.
In an area model, one shape represents the whole. The whole is divided into fractional regions. Although the fractional regions are equal in area, they are not necessarily congruent (the same size and shape).
5. Strategies by Concepts - Holly
Operations
Ensure that essential prior understanding is in place - do not introduce concepts prematurely
Build on students understanding of operations with whole numbers
E.g. addition can only occur between quantities with like units
Equivalence and Comparing
Connect fractions with other number systems for equivalence
Change the wholes so that students learn to consider the whole, the numerator and the denominator
Determine equivalent fractions through splitting and merging by using models before moving the the abstract
Representations
Avoid using circles in P/J since students do not learn area of a circle until intermediate and since circles are difficult to equi-partition in multiple ways
Use both continuous representations (area, volume, number line) and discrete representations (sets)
New concept = use familiar representations
Familiar concept = use new representations
Use representations that can be used at any grade level for a number of problems and purposes
E.g. number lines, rectangles, fraction bars, number rods
Use whole numbers to introduce notation along with picture representations
Unit Fractions
Emma - I like that unit fractions can be used as a starting point when teaching about fractions. Using unit fractions as benchmarks for referencing is a good strategy to teach students, and using models and pictures to demonstrate these parts of a whole in a concrete way will help learners get a better understanding of this new concept.
Must use precise language - all fractions should be read as a number
E.g. the fraction 5/4 is read as five-fourths, NOT five over four, five out of four, five-quarters
Introduce both mixed and improper fractions
Help develop fractional number sense
Use benchmarks for referencing
Compose and decompose fractions into unit fractions
Count by unit fractions to familiarize with numerator and denominator
Create unit fractions through equi-partitioning a whole
As teachers: avoid providing pre-partitioned figures
Iterating - copying or combining equal units to create a new fraction or the whole
Use of physical models, pictures and numbers.
4 Constructs (Alysha and Adam)
Jovana- I think the differentiation between part-part fractions and part-whole fractions is very interesting. Personally, in primary school we focused on part-whole fractions. Instinctively, when I think of fractions I think of parts of a whole or part of 1 so the fraction 3/2 would be 1 and a half rather than three oranges and two non-oranges and the total of the numerator and denominator is the total amount of fruit. Once we got into ratios, I learned to communicate part-part fractions as 3:2. It's important to be consistent when teaching math and to remember that students connect to various methods of explanation so introducing this method in primary could be very useful.
Part-Part Relationships:
A fraction can also be used to represent a part-part relationship.
Three ways to think about Part-Part Relationships.
Set Model
In the set of pieces of fruit, the number of pieces of fruit that are apples is 2/6 the number of pieces that are not apples.
Area Model
In the rectangle, 7/2 as many regions are shaded as are unshaded.
Number Line Model
Number Lines show a part-part relationship in which the distance a flag is hoisted up a pole.
Part-Whole Relationships
Learners are most familiar with the part-whole construct of fractions in which the denominator indicates the number of fractional units being counted.
Set Models Representing Part-Whole Relationships
When looking at a set of objects, it is important to be explicit about what is considered a whole.
Example: A whole is a carton of 12 eggs.
Number Line Model Representing Part-Whole Relationships
A fraction on a number line, as shown, is another example of a part whole relationship.
Quotients and operators can be derived from all types of fractions: proper, improper, unit and mixed
Fractiosn as Operators
Enlarging or shrinking a quantity by a factor
Illustrations can be used to simplify complex questions. For example, if half of a lasagna is left and dad eats two-thirds of the remainder, how much of the whole lasagna is left?
Illustration (CONCRETE)
Algorithm (ABSTRACT) 1/3 x 1/2 = 1/6
ENLARGING E.g., Walking one and a half times as far (1 1/2) on Tuesday as on Monday
SHRINKING E.g., one-third (1/3) of an object
Fractions as Quotients
Dividing the numerator by the denominator
The result is the decimal equivalent for the fraction
The context of the question suggests equal sharing
Students introduced to the concept through equal-share contexts
Important for teachers to be precise depending on the construct of the fraction
E.g. in 3/2, the numerator is the WHOLE, and the denominator is the PARTITION
Example
This can also be represented on a number line
This is only one way to divide up the brownies. Other options include giving one brownie to each person and partitioning the remaining two or partitioning the brownies equally into four parts.