作者:YURIDIA VILLANUEVA DIAZ 3 年以前
184
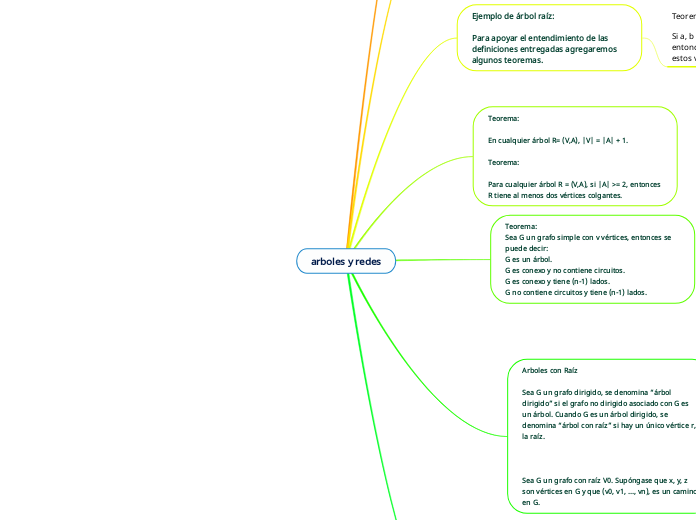
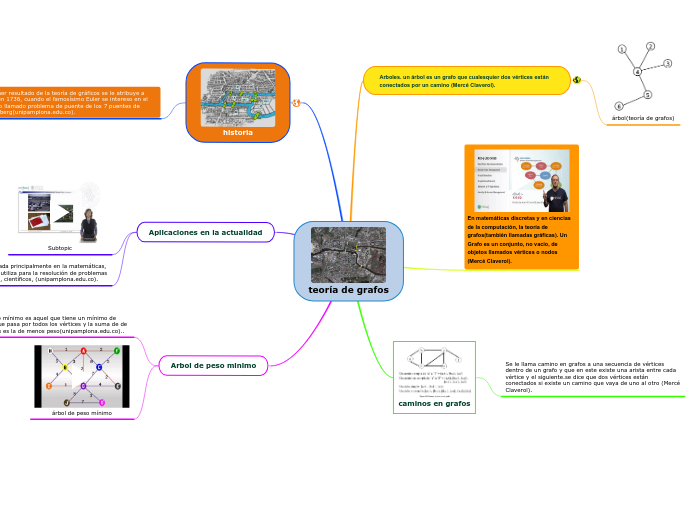
arboles y redes
Un árbol es un grafo simple que no contiene ciclos y es conexo, es decir, existe un único camino entre cada par de vértices. En los árboles, la cantidad de vértices siempre es igual al número de aristas más uno.