Basic Measurement: Perimeter, Area, Volume, and Surface Area
The purpose of this mind map is provide resources for exploring and clarifying the topic. The audience is elementary students.
surface area (SA)
Surface Area (SA or S) is the boundary of a space figure. A space figure is an object that is represented in three dimensions (3D).
Total surface area is the sum of the base area and lateral area (or sides) of a space figure.
Think about a jacket or cover that would enclose the entire shape.
SA of a shpere
Surface Area of a Sphere:
SA=4πr2
Let r be the radius of the sphere.
watch this video to see how the surface area of a sphere is estimated by thinking of a number of small
bases covering the sphere
SA of a cone
Surface Area of a Right Circular Cone:
SA=πr2+πrs
Let s be the slant height and r be the radius of the base.
Note: to determine slant height use the Pythagorean Theorem: s= √(x2-y2) given x is the height of the cone and y is the radius of the cone. When thinking about this triangle let s be the hypotenuse, and x and y be the two legs.
SA of right rectangular pyramid
Surface Area of a Right Regular Pyramid:
SA=B+(1/2)ps
Let s be the slant height, and B be the base area, and p be the perimeter of the base.
Note: to determine slant height use the Pythagorean Theorem: s= √(x2-y2) given x is the height of the pyramid and y is the (1/2) the length of one side of the base of the pyramid. When thinking about this triangle let s be the hypotenuse, and x and y be the two legs.
click the link to explore the surface area of pyramids
SA of a cylinder
Surface Area of Right Prism or Cylinder:
SA=2B+ph
Let h be the height, and B be the areas of both bases, and p be the perimeter of each base.
Note: if you unroll the side of a cylinder you have a rectangle
click the link to see the side of a cylinder unrolled
SA of right prism
Surface Area of Right Prism or Cylinder:
SA=2B+ph
Let h be the height, and B be the areas of both bases, and p be the perimeter of each base.
Note: if you unfold a prism you have a collection of 2D shapes called the net of the prism
click the link to see the nets of some
rectangular prisms
volume (V)
Volume is the amount of space enclosed within the boundary of a 3D shape (or object).
volume of a sphere
Volume of a sphere: V=(4/3)πr3
where r is the radius of the sphere
Note: the volume of a sphere takes up (2/3) the volume of a cylinder of the same radius and diameter height
click the link to use a sphere volume calculator and a table of radius to volume values
volume of a pyramid or cone
Volume of pyramid or cone: V=(1/3)Bh where B is the area of the base and h is the height.
Notes: a pyramid will fill (1/3) of a rectangular prism with the same base and height
a cone will fill (1/3) of a cylinder with the same base and height
click the link to watch a video explanation
of volume of a pyramid
volume of a cylinder
Volume of a cylinder: V=Bh where B is the area of the base and h is the height.
Notes: the base of a cylinder is a circle
this same formula is used to find the volume of right, oblique, or general cylinders!
volume of a box
The volume of a rectangular box (or prism) is found by multiplying length x width x height.
Use the formula: V=Bh where B is the area of the base and h is the height.
Note: to find the volume of a complicated prism, decompose it into simpler shapes (watch the video to see a demonstration of this)
click on the video to hear a song about volume of rectangular prisms
Pythagorean Math
theorem
a2 + b2 = c2
The sum of the areas of squares on the legs of a right triangle is equal to the square on the hypotenuse.
click on the link to explore the Pythagorean Theorem
Uses
Right triangle
If a2 + b2 = c2
then it IS a right triangle.
If a2 + b2 ≠ c2
then it IS NOT a right triangle.
unknown side
If two sides of a right triangle are known, then the length of any unknown side can be found using the theorem a2 + b2 = c2
slant height
The slant height of a cone can be determined by thinking about a triangle where one leg is the radius of the base and the other leg is the vertical height of the cone, the slant height would be the hypotenuse.
Thus: Slant Height2=h2+r2
where h is the vertical height and r is the radius of the cone
The Measurement Process
Units
U.S. Customary System of Units
U.S. units of capacity
capacity conversions
U.S. units of volume
Units of volume will be the unit of measurement cubed, for example the volume of a rectangular prism measured in inches will be given as ___ cubic inches (or in.3).
This is because there are three measurements used to calculate volume: length, width, and height. We are considering three dimensions of the object, think 3D therefore cubed.
U.S. units of area
Units of area will be the unit of measurement squared, for example the area of a rectangle measured in inches will be given as ___ square inches (or in.2).
This is because we are considering two dimensions of the object: length and width. Think 2D therefore squared.
U.S. units of length
click on the link to view customary units of length with
picture examples
International System of Units
metric units of volume
click on the link, or watch the video, for a look at converting between liters and milliliters
metric units of area
click on the link for picture examples and a great explanation of metric a
rea units
SI prefixes
Four steps
4. express as number of units
4. Express the measurement as the number of units used in the comparison.
3. make a comparison
3. Use a measurement device to compare the object to the unit of measurement.
A measurement device is a tool or instrument used to measure: ruler, tape measure, meter stick, gauge, scale, thermometer, etc.
2. select a unit
2. Select an appropriate unit of measurement.
The unit of measure will change based on what you are measuring. Possibilities for measuring length include, but are not limited to: inches, feet, miles, centimeters, meters, kilometers
For weight you could use: ounces, pounds, tons, milligrams, grams, or kilograms.
Remember to chose a unit that makes sense for what you are measuring.
1. choose an attribute
- Choose the attribute to be measured: length, area, volume, capacity, temperature, time, or weight.
perimeter (P)
The perimeter of a region is the length of its boundary, just the outer edge of a 2D shape (or region).
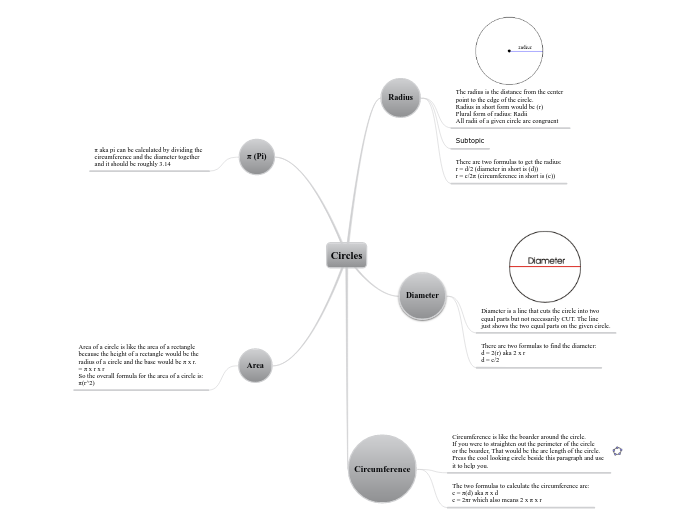
perimeter of a circle
The perimeter of a circle is called its circumference.
It is found with the formula C=2πr where C is the circumference and r is the radius of the circle.
Perimeter of polygons
To find the perimeter of a polygon add the lengths of all of its sides.
For example: if I have a square with side lengths of 3 ft., I will add 3+3+3+3= 12 ft.
area (A)
The area of a region is the amount of space inside the boundary (or perimeter) of a 2D object. Think about the number of tiles required to fill a shape with no overlapping.
area of circles
Area of a circle: A=πr2 where r is the radius of the circle.
click the link for area of a circle practice problems
area of trapezoid
Area of trapezoid: A=(1/2)(a+b)h
where a and b are the lengths of the two bases and h is the height of the trapezoid
area of triangles
Area of triangle: A=(1/2)bh
(Area = one half Base x Height)
click on the link to see how two congruent triangles form a parallelogram
area of parallelograms
Area of parallelogram: A=bh (Area=base x height)
click the video link to watch how a the area of a parallelogram can be transformed to make a rectangle of equal area
area of rectangles
For all rectangles: A=wl (Area = Width x Length)
click the link to read about the area of rectangles, and to
watch a video tutorial