VM266 7337
Theorem 7.6
if f is continuous and increasing on [a.b] the f have an inverse function
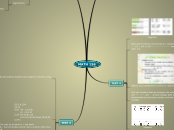
Theorem 7.7
derivative of inverse function
the derivative of the inverse function g is the reciprocal of the derivative f
if a diffrentiable function f has an inverse function and if f'(g(c)) does not equal 0 then g is differentiable at c
Converse
Theorem 7.3
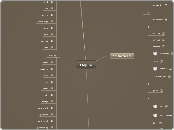
g: R -> D
f: D -> R
P <=> Q
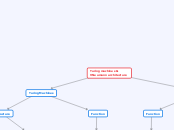
Inverse Functions Pairs
One to One
Increasing or Decreasing
determine the slope of the funtion
f: D -> R is incresing for every D
One input - One output
unique fn
Horizontal Line Test
g=f^-1
conditions
g(f(x)) = x for every x in D
f^-1(f(x)) = X FOR EVERY X IN DOMAIN OF F
f(g(x)) = y for evey y in R
f(f^-1(x)) = X FOR EVERY X IN DOMAIN OF F^-1
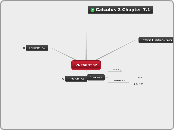
Calculus 2 Chapter 7.1