CREADO POR : Mayra Rosero
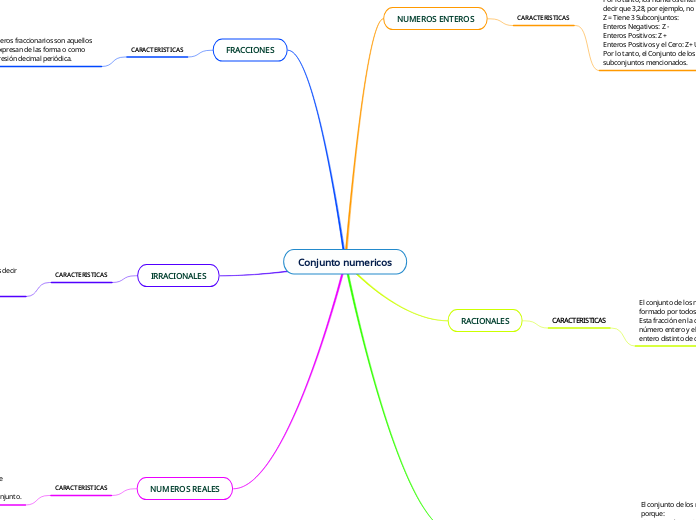
Conjunto numericos
NATURALES
El conjunto de los números naturales se caracteriza porque:
Tiene un número infinito de elementos
Cada elemento tiene un sucesor y todos, excepto el 1, un antecesor.
El sucesor de un número natural se obtiene sumando uno (+1); el antecesor se obtiene restando uno (-1).
POTENCIACION
Es multiplicar varias veces el mismo número por sí mismo. El número que multiplicamos se llama base, y el exponente es el número de veces que se multiplica.
Por ejemplo, 2 · 2 · 2 · 2 · 2= 25 = 32. Aquí, la base es 2, el exponente 5 y el resultado, 32.
Cuadrados perfectos: son los números naturales al cuadrado.
Por ejemplo, 22=4, 32=9, 42=16, 52=25, 62=36, 72=49, 82=64, 92=81, etc.
Y de la misma forma, los cubos perfectos serían: 23=8, 33=27, 43=64, 53=125, etc.
N = { 1, 2, 3, 4, 5, 6, 7,.......}
Puesto que los números naturales se utilizan para contar elementos, el cero puede considerarse el número que corresponde a la ausencia de los mismos; dependiendo del área de la ciencia, el conjunto de los números naturales puede presentarse entonces de dos maneras distintas:
Definición sin el cero:{N} :1,2,3,4,5,6,7,8,9,10,
Definición con el cero: {N} :0,1,2,3,4,
En el conjunto de los números naturales se pueden definir distintas operaciones como la suma (adición), la resta (sustracción), la división y la multiplicación. También se pueden establecer relaciones de orden como son mayor que, igual que, o menor que.
RACIONALES
El conjunto de los números racionales está formado por todos los números de la forma a/b. Esta fracción en la cual el numerador es a, es un número entero y el denominador b, es un número entero distinto de cero.
Q = {....- ¾, - ½, - ¼ , 0, ¼ , ½, ¾,.....}
Las operaciones fundamentales en este conjunto son la suma y la multiplicación. La diferencia (o resta) y la división de fracciones son operaciones que dependen de las dos fundamentales.
El conjunto que engloba a los números enteros y a los fraccionarios positivos y negativos conforma el conjunto de los números racionales, que se denota por Q.
NUMEROS ENTEROS
Los números enteros abarcan a los números naturales (los que se utilizan para contar los elementos de un conjunto), incluyendo al cero y a los números negativos (que son el resultado de restar a un número natural otro mayor). Por lo tanto, los números enteros son aquellos que no tienen parte decimal (es decir que 3,28, por ejemplo, no es un número entero).
Z = Tiene 3 Subconjuntos:
Enteros Negativos: Z ¯
Enteros Positivos: Z +
Enteros Positivos y el Cero: Z+ U {0}
Por lo tanto, el Conjunto de los números enteros es la unión de los tres subconjuntos mencionados.
EJEMPLO
Son cualquier número natural: 1, 2, 3, 4, 5, 10, 125, 590, 1926, 76409, 9.483.920, junto con cada número negativo correspondiente: -1,-2, -3, -4, -5,-10, -590, -1926, -76409, -9.483.920. Esto incluye, claro, al cero (0). - Fuente: https://concepto.de/numeros-enteros/
Hay tres operaciones entre números enteros que tienen como resultado números enteros: la suma, la resta y la multiplicación.
DIVISIBILIDAD DE LOS NUMEROS ENTEROS
Se dice que un número a es divisible entre otro número b si la división a entre b es exacta, es decir, si a es un múltiplo de b ( a=nb, n Î Z ). También se dice que b es divisor de a. En ocasiones se representa que un número a es divisible entre otro b mediante el siguiente símbolo matemático: a ½ b. La divisibilidad es una propiedad importante en aritmética. De ella que se derivan conceptos como el de número primo, máximo común divisor o mínimo común múltiplo, y Ejemplo: 15 es divisible por 3, porque 15:3=5 y el resto es cero, pero 9 no es divisible por 2 porque 9:2 es 4 con resto 1.
DESCOMPOSICION DE NUMEROS PRIMOS
Todo número compuesto se puede escribir como multiplicación de dos o más factores primos.
Para descomponer un número en producto de factores primos se siguen estos pasos:
1° Se escribe el número a la izquierda de una raya vertical (actúa como "ventana" de división) y a su derecha el menor número primo (2, 3, 5, 7,... ) por el cual dicho número sea divisible. El cociente obtenido se coloca debajo del número propuesto.
2° Se procede como en el paso anterior con el cociente obtenido, y así sucesivamente hasta llegar a un cociente igual a 1.
MCM
MINIMO COMUN MULTIPLO El mcm de dos o más números es el menor de los múltiplos comunes positivos, excluyendo el 0.
Para su cálculo descomponemos los números en sus fcatores primos y multiplicamos los comunes y no comunes con el mayor exponente.
MCD
MÁXIMO COMÚN DIVISOR (MCD
El MCD de dos o más números es el mayor de los divisores comunes.
Para su cálculo descomponemos los números en sus factores primos y multiplicamos los comunes con el menor exponente.
Los números enteros se representan en una recta numérica, teniendo el cero en medio y los números positivos (Z+) hacia la derecha y los negativos (Z-) Z = { ..... –3, -2, -1, 0, 1, 2, 3,...}
NUMEROS REALES
Surgen de la necesidad de reunir los racionales y los irracionales en un solo conjunto.
R = {....- 10, -1, - ¾, - ½, - ¼, 0, ¼ , √2, 5 , .....}
Existen cuatro operaciones básicas de los números reales, a saber suma, resta, multiplicación y división. Al realizar ejercicios de cada una de ellas es muy importante considerar el signo de cada operación.
Los números reales se expresan con decimales que tienen una secuencia infinita de dígitos a la derecha de la coma decimal, como por ejemplo 324,8232.
IRRACIONALES
Este conjunto pertenecen todos los números decimales infinitos puros, es decir aquellos números que no pueden transformarse en una fracción.
π (pi). Es el número irracional más conocido.
√5. 2.2360679775
√123. 11.0905365064
Las operaciones de suma, resta, multiplicación y división no son operaciones bien definidas en los números irracionales, dados dos números irracionales no siempre la suma, resta, multiplicación o división de dichos números resulta un número irracional.
La representación gráfica de los números irracionales se la hace con la letras mayúsculas así: R - Q. Se la utiliza de esta manera para diferenciarla de los números imaginarios, cuya representación es la i minúscula. Pero el símbolo no se representa en las ecuaciones al no constituir una estructura algebraica, y para no crear confusión, en ocasiones se los puede ver como R/Q como la representación de números irracionales por definición.
FRACCIONES
CARACTERISTICAS
Los números fraccionarios son aquellos que se expresan de las forma o como una expresión decimal periódica.
EJEMPLOS
3 2/5 (tres enteros y dos quintos)
1 2/3 (Un entero y 2 tercios)
45 74/100 (cuarenta y cinco enteros y setenta y cuatro centésimos)
62 3/8 (sesenta y dos enteros y tres octavos)
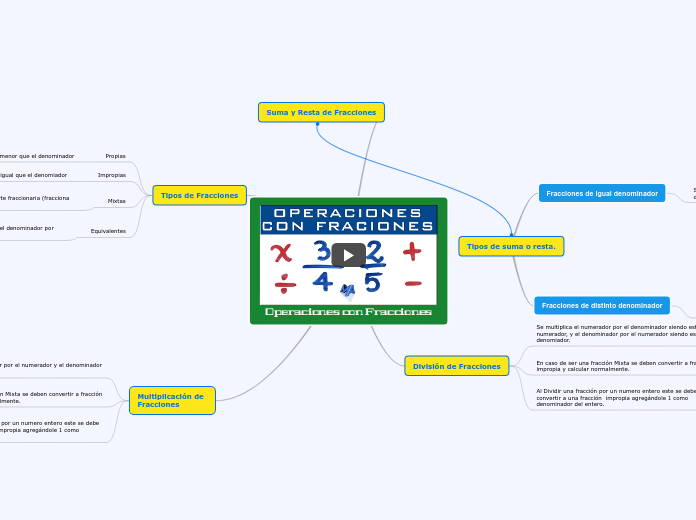
OPERACIONES
Operaciones con fracciones : suma, resta, multiplicación y división de fracciones
NOTACION
Q+ = { 0, ½ , 2, 3/4 3, 9/7,.....} Las fracciones comunes se pueden expresar en notación decimal. El número que se encuentra a la izquierda de la coma es la parte entera y las cifras que quedan situadas a la derecha de la coma son la parte decimal.