DERIVADA

更多类似内容

inventos antes del computador

由Joan Gabriel Acevedo Mateus

6º Primaria. Los organos de los sentidos.

由Celia Flores

Límites

由Lucas Salbatierra

ORGANISMOS DE CONTROL

由edisson gomez

Pérez Cruz Alejandro de Jesús 4APRV

Las indeterminaciones en los límites son las expresiones que no quedan al sustituir la x por el número al que tiende y que no tienen solución. En todas ellas, están involucradas de alguna forma el cero o el infinito.

Si f(x) es una función usual (polinómicas, racionales, radicales, exponenciales, logarítmicas, etc.) y está definida en el punto a, entonces se suele cumplir que: lim f(x)=f(a) x → a Es decir: para calcular el límite se sustituye en la función el valor al que tienden las x.

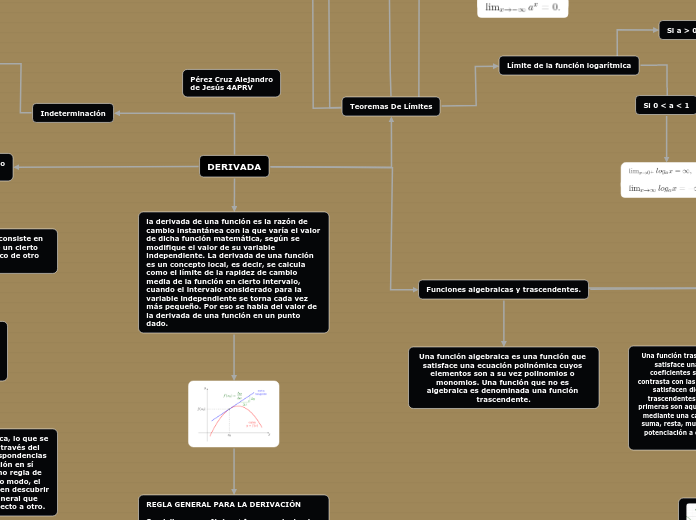
DERIVADA

la derivada de una función es la razón de cambio instantánea con la que varía el valor de dicha función matemática, según se modifique el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por eso se habla del valor de la derivada de una función en un punto dado.

Indeterminación

Teoremas De Límites

Límite de la función logarítmica

Si a > 0

-

Límite de la función exponencial

Si 0 < a < 1

a

Si a > 1

.

Límite cuando x tiende a infinito

Límite cuando x tiende a menos infinito

Cuando x → ∞ se tiene que:

Para calcular el límite de una función cuando x →∞ se sustituyen las x por ∞.

El límite cuando x → ∞ de una función polinómica es ±∞ dependiendo de si el término de mayor grado es positivo o negativo.

Límite en una función definida a trozos

Para estudiar el límite de una función definida a trozos, en primer lugar tenemos que estudiar los límites laterales en los puntos de unión de los diferentes trozos. Después, si estos coinciden, este es el valor del límite, si no coinciden, el límite no existe.

Un ejemplo de una función donde los limites laterales si coinciden es la siguiente

Límite en un punto

Funciones algebraicas y trascendentes.

Función de varias variables

Función continúa y discontinua

una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función Las Funciones Discontinuas son aquellas funciones en las que existen saltos o están rotas en alguna parte de su trazo.

Incremento de una función

La palabra incremento se entiende como el aumento del valor de una variable. El incremento Δx de una variable x es el cambio en x cuando esta crece o decrece desde un valor x = x1, hasta un valor x = x2 y se escribe Δx = x2 = x1

Las funciones de varias variables son funciones como cualquier otra, cumplen la misma definición de función; una relación. La diferencia es que una variable dependiente estará regida por más de una variables independiente. Es muy común trabajar con funciones de tres variables, generalmente llamadas z = f(x,y). La idea de relación es más compleja puesto que el valor de z depende no solo del valor de x o de y, sino de puntos coordenados a los que les corresponde un valor de z.

Una función trascendente es una función que no satisface una ecuación polinómica cuyos coeficientes sean a su vez polinomios; esto contrasta con las funciones algebraicas, las cuales satisfacen dicha ecuación.1 Se dividen en trascendentes elementales y superiores. Las primeras son aquellas que pueden ser expresadas mediante una cantidad finita de operaciones de suma, resta, multiplicación, división, radicación, potenciación a exponentes constantes reales y logaritmación

Una función algebraica es una función que satisface una ecuación polinómica cuyos elementos son a su vez polinomios o monomios. Una función que no es algebraica es denominada una función trascendente.

Regla de asignación o correspondencia.

Una regla de correspondencia consiste en asignar un elemento único de un cierto conjunto a cada elemento único de otro conjunto.