作者:jaime alvarado 1 年以前
105
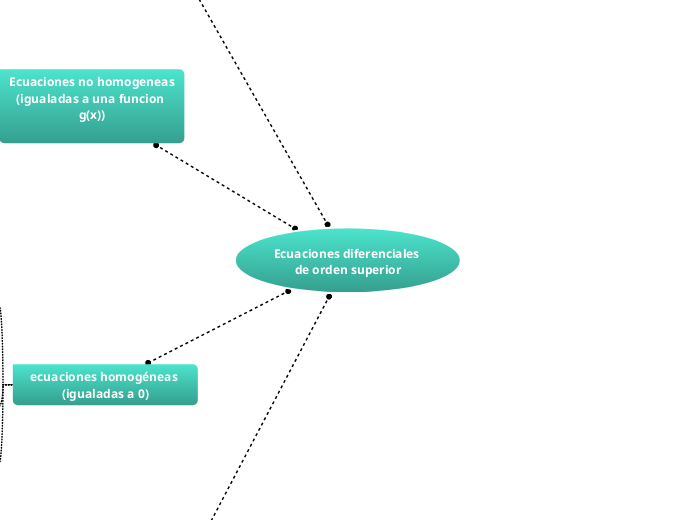
Ecuaciones diferenciales de orden superior
Las ecuaciones diferenciales de orden superior son un área fundamental en matemáticas aplicadas y su estudio incluye tanto ecuaciones homogéneas como no homogéneas. Estas últimas son igualadas a una función arbitraria g(