作者:ARANZAZU RAMIREZ ATONAL 2 年以前
136
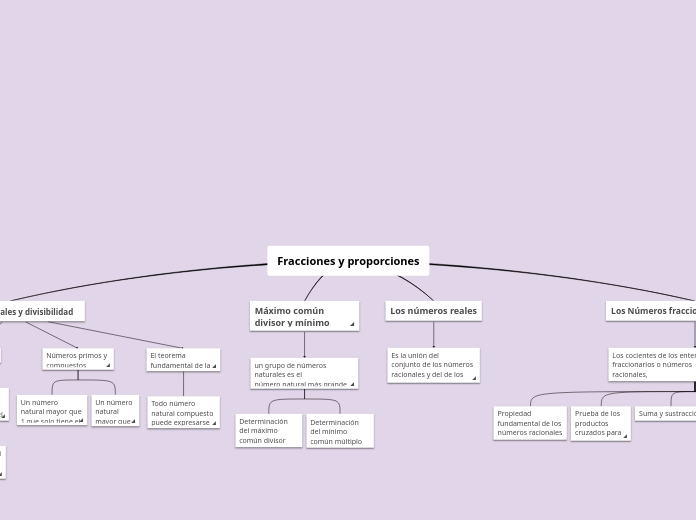
Fracciones y proporciones
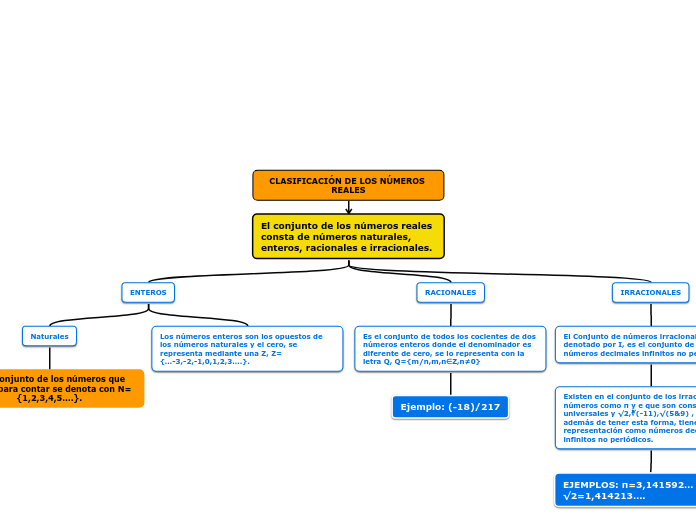
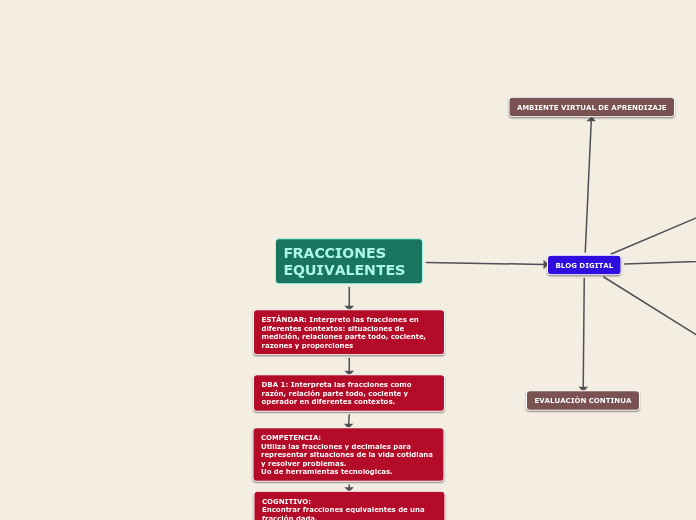
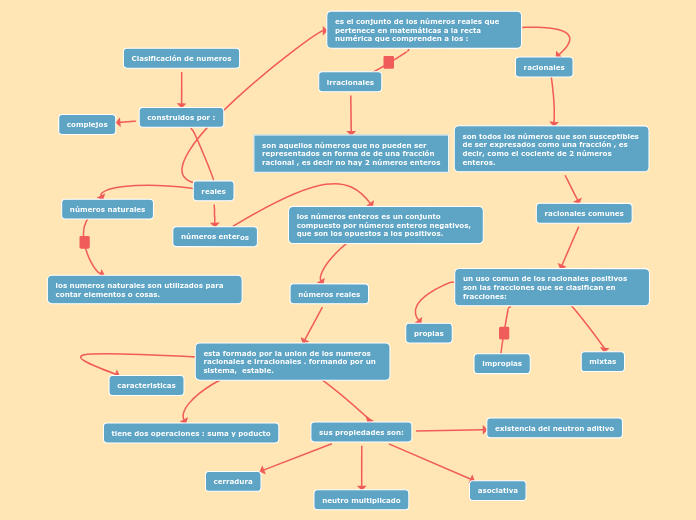
Los números fraccionarios y decimales son fundamentales en matemáticas, especialmente cuando se trata de la igualdad de números racionales mediante productos cruzados. La comprensión de los números fraccionarios, también conocidos como racionales, implica la suma, la sustracción, la multiplicación y la división.