funzione

更多类似内容

portfolio-Enrica Portas

由Enrica Portas

La Funzione matematica

由Malina Lungu

Sample Mind Map

由ciro gamen

ORARIO

由Sabrina Pensili

Funzioni

Limiti

Asintoti

Orizzontale

Si dice che la retta y=l è un asintoto orizzontale per la funzione f se si verifica una almeno delle seguenti condizioni:
f(x) = l oppure f(x) = l
Ove l è un numero reale. In pratica la curva si accosta sempre più ad una retta di equazione y=l ed in questo caso è il numero l quel che dobbiamo determinare.

Verticale

Si dice che la retta x = c è un asintoto verticale per la funzione f se c'è un punto singolare in cui si abbia:
f(x) = ± oppure f(x) = ±
In pratica la curva si accosta sempre più ad una retta di equazione x = c ed è il valore c (se esiste) ciò che dobbiamo determinare (pertanto una funzione che non abbia punti singolari non può avere asintoti verticali).

Si dice che l'asintoto è pari se lim f(x)=± per x che tende a c sia da sx che da dx, e dispari se i limiti sono discordi.

Obliqui

Se si ha f(x)= ± oppure f(x)= ±, è lecito chiedersi se esista un asintoto obliquo, e cioè se il grafico della funzione si accosta (quando x tende a più o meno infinito) a quello di una retta di equazione y=mx+q (ove m ¹ 0, altrimenti si tratterebbe di un asintoto orizzontale); naturalmente possiamo avere due diversi asintoti obliqui per x che tende a più o meno infinito. Quindi in questo caso dobbiamo determinare (se esistono) i valori m e q.
Per determinare m si calcola il limite: . Se tale limite esiste ed è finito, ci dà il valore di m; si procede allora a calcolare q effettuando il limite f(x) - mx .
Di nuovo, se tale limite esiste ed è finito, esso ci dà il valore di q. e quindi l'asintoto obliquo esiste per x che tende a più infinito ed ha equazione y=mx+q . Lo stesso tipo di analisi va compiuto per x che tende a meno infinito.

Il limite di una funzione è uno dei concetti di base dell'analisi matematica. Se una funzione è una legge che associa a un elemento x di un insieme numerico un altro elemento y = f(x), allora ha senso chiedersi cosa accade quando ci si avvicina sempre di più a un certo numero x0.

Con il calcolo dei limiti viene definita la continuità di una funzione, la sua discontinuità, la derivata. Si tratta di una nozione fondamentale non solo in matematica, ma anche in molti altri settori della scienza.

In questo corso i limiti di funzione vengono trattati con 12 video, in cui la spiegazione delle basi teoriche è costantemente accompagnata da pratici esempi ed esercizi svolti.

Dopo aver introdotto il concetto di limite e di continuità in un punto, vengono definiti:

- I limiti di funzione razionale fratta quando la variabile tende a un valore preciso x0 oppure quando tende a +∞;
- Le forme indeterminate;
- I limiti delle funzioni composte;

Pari e Dispari

Una funzione si dice pari se cambiando di segno la x la funzione non cambia di segno in formula: f ( - x ) = f ( x )

In pratica significa che una funzione pari e' simmetrica rispetto all'asse y, cioe' i valori a destra dell'origine sono uguali a quelli a sinistra.
Un esempio semplice di funzione pari e' dato da
y = x 2
infatti il quadrato mi rende positivo il risultato sia che alla x sostituisca un numero positivo che negativo
Per le funzioni pari bastera' costruire solo meta' grafico poi farne il simmetrico rispetto all'asse delle y (simmetria assiale). In pratica lo ribalto attorno all'asse y. In blu la parte ribaltata

Una funzione si dice dispari se cambiando di segno la x anche la funzione cambia di segno in formula: f ( - x ) = - f (x)

In pratica significa che una funzione dispari e' simmetrica rispetto all'origine, cioe' i valori a destra dell'origine sono uguali a quelli a sinistra cambiati di segno.
Un esempio semplice di funzione dispari e' dato da
y = x 3
infatti il cubo mi rende positivo il risultato se alla x sostituisco un numero positivo e negativo quando alla x sostituisco un valore negativo
Anche per le funzioni dispari bastera' costruire solo meta' grafico poi farne il simmetrico rispetto all'origine (simmetria centrale). In pratica lo ribalto prima attorno all'asse y e poi attorno all'asse x. In blu la parte ribaltata due volte

Segno

Disequazioni

Come hai visto per alcune disequazioni di secondo grado potremmo usare la scomposizione in fattori di primo grado, pero' vi sono delle equazioni che non sono scomponibili Quindi e' necessario elaborare un metodo generale per determinare sempre il segno delle disequazioni di secondo grado Vi sono due metodi, uno piu' razionale e l'altro piu' intuitivo;

DISEQUAZIONE DI PRIMO GRADO :una disequazione si dice di primo grado quando le incognite vi compaiono a potenza 1

Ad esempio:
x + 2y - 3z - 4 3x +2y
e' una disequazione di primo grado a tre incognite (x, y e z)
Qui e in seguito trattiamo essenzialmente le disequazioni ad una incognita, ma facciamo anche un cenno a quelle a piu' incognite

La disequazione e' una diseguaglianza che e' verificata per certi intervalli di valori

Ad esempio la disequazione
x - 4 0
e' verificata per tutti i valori della x maggiori di 4, cioe' se al posto della x metto 5, 6, oppure 4,111... e' vero che il primo termine della disuguaglianza e' maggiore o uguale al secondo
Risolvere una disequazione significa trovare gli intervalli dei valori che sostituiti alla x rendono la diseguaglianza vera
In una disequazione possiamo trovare solo i valori maggiori oppure minori di qualcosa
oppure possiamo trovare i valori maggiori e uguali oppure minori e uguali .
Occorre fare molta attenzione e considerare sempre se devo o no prendere il valore corrispondente all'uguale
Se fai confusione fra i segni maggiore e minore

Studio di funzioni

Definizione di segno

Definizione di pari e dispari

Definizione di Codominio

Esempi

link utili

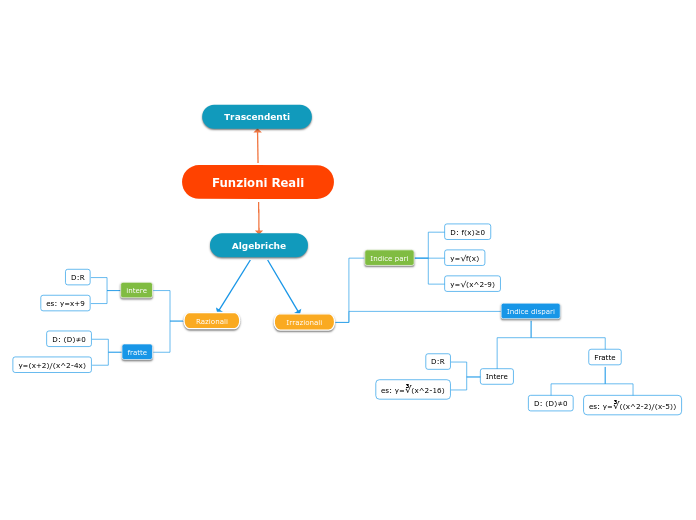
Studio

Dominio: si dice dominio di una funzione f(x) l'insieme dei valori possibili che la variabile indipendente x può assumere,in modo che la funzione sia definita in tali valori.

tipologie di funzioni algebriche

irrazionali

relazionali fratte

relazionali intere

tipologie funzioni trascendenti

funzione esponenziale con base maggiore di 1

funzione esponenziale con base compresa tra 0 e 1

funzione logaritmica, associa a ogni numero reale positivo per il suo logaritmo in base a

E' una relazione che associa due elementi appartenenti a due gruppi.