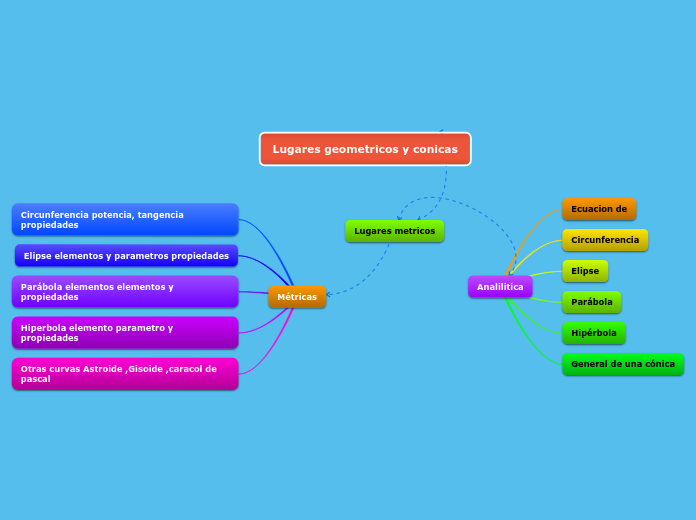
LAS DIFERENTES CONICAS
EJEMPLOS
X2/a2-y2/b2=1
X/B2+Y2/a2=1
PARABOLA
(y-k)2=4p(x-h)
(x-h)2=4p(y-k)
CIRCUNFERENCIA
(X-H)2(Y-K)2=R2
JULIAN SANTIAGO RICO MEDINA ,CARLOS ANDRES CARDOCO MORO,ANDRES FELIPE PEDREROS SANABRIA CURSO:1103
INSTITUCION EDUCATIVA POLITECNICO ALVARO GONZALEZ SANTANA
CICUNFERENCIA
HIPERBOLE
Curva simétrica respecto de dos ejes perpendiculares entre sí, compuesta de dos ramas abiertas, dirigidas en sentidos opuestos, que se aproximan indefinidamente a dos asíntotas, de modo tal que la diferencia de sus distancias a dos puntos fijos es siempre constante.
MATEMÁTICAS
Eje secundario o imaginario: Es la mediatriz del segmento FF'.
Eje principal o real: Es la recta que pasa por los focos.
ELIPSE
Figura geométrica curva y cerrada, con dos ejes perpendiculares desiguales, que resulta de cortar la superficie de un cono por un plano no perpendicular a su eje, y que tiene la forma de un círculo achatado.
Eje secundario: Es la mediatriz del segmento FF'.
Eje focal: Es la recta que pasa por los focos
Focos: Son los puntos fijos F y F'.
Una circunferencia corresponde al conjunto de todos los puntos equidistantes (es decir, están siempre a la misma distancia) de un punto fijo que llamaremos centro. A este centro le llamaremos O, y la distancia que separa O del conjunto de puntos, la llamaremos R.
Diámetro: mayor cuerda que une dos puntos de una circunferencia. Hay infinitos diámetros y todos pasan por el centro de la circunferencia.
Radio: pedazo de recta que une el centro con cualquier punto perteneciente a la circunferencia.
Centro: punto central que está a la misma distancia de todos los puntos pertenecientes a la circunferencia.
PARÁBOLA
Curva abierta formada por dos líneas o ramas simétricas respecto de un eje y en que todos sus puntos están a la misma distancia del foco (un punto) y de la directriz (recta perpendicular al eje).
Parámetro: A la distancia entre el foco y la directriz de una parábola se le llama parámetro .
Directriz: Es la recta fija .
Foco: Es el punto fijo .