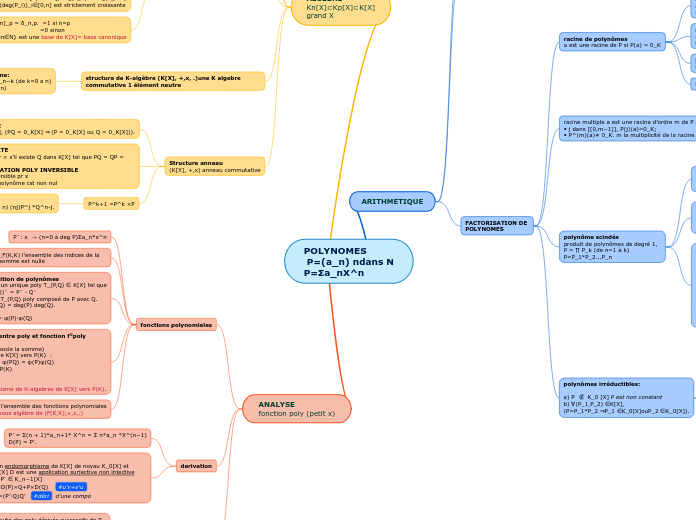
POLYNOMES
P=(a_n) ndans N
P=Σa_nX^n
ANALYSE
fonction poly (petit x)
derivations successives
FORMULE DE TAYLOR ALGEBRIQUE
P=Σ(P^k)(a)/k! * (X-a)^k
P≠0_K[X]
P=(de 0 à deg(P))ΣP^(k)(a)*(X−a)^k/k!
FORMULE DE LEIBNIZ
(PQ)^n=Σ(nj)P^j Q^(n-j)
(P(^n))_n∈N la suite des poly dérivés successifs de P
P^0=P
P(n+1) =D(P(n)).
derivation
PPTE:
1) D est un endomorphisme de K[X] de noyau K_0[X] et d’image K[X] D est une application surjective non injective
2) D(P) = P′ ∈ K_n−1[X]
3) D(PQ)=D(P)×Q+P×D(Q) #u'v+v'u
4) D(P◦Q)=(P′◦Q)Q′ #déri d'une compo
P′ = Σ(n + 1)*a_n+1* X^n = Σ n*a_n *X^(n−1)
D(P) = P′.
fonctions polynomiales
P(K) l'ensemble des fonctions polynomiales
une sous algèbre de (F(K,K),+,x,.)
correspondance entre poly et fonction f°poly
φ : K[X] → P(K)
P→ P˜ (associe la somme)
un isomorphisme de K[X] vers P(K) :
1) ∀(P,Q) ∈ K[X]2, φ(PQ) = φ(P)φ(Q)
2) φ(1_K[X]) = 1_P(K)
3) φ∈L(K[X],P(K))
4) φ est bijectif
φ est un isomorphisme de K-algebres de K[X] vers P(K).
composition de polynômes
Il existe un unique poly T_(P,Q) ∈ K[X] tel que
(T_(P,Q))˜ = P˜ ◦ Q˜
P ◦ Q = T_(P,Q) poly composé de P avec Q.
deg(P ◦ Q) = deg(P) deg(Q).
φ(P◦Q) = φ(P)◦φ(Q)
P = 0_K[X], alors P˜= 0_F(K,K) l’ensemble des indices de la somme est vide donc la somme est nulle
P˜: x → (n=0 à deg P)Σa_n*x^n
ALGEBRE
Kn[X]⊂Kp[X]⊂K[X]
grand X
Structure anneau
(K[X], +,x) anneau commutative
P^k+1 =P^k ×P
FORMULE DU BINOME
∀n∈N, (P+Q)^n=Σ(de j=0 à n) (nj)P^j *Q^n-j.
INVERSIBILITE
inversible pour × s’il existe Q dans K[X] tel que PQ = QP = 1_K[X].
CARACTERISATION POLY INVERSIBLE
lasse 1) P inversible pr x
2) P un polynôme cst non nul
INTEGRITE
∀P,Q ∈ K[X], (PQ = 0_K[X] ⇒ (P = 0_K[X] ou Q = 0_K[X])).
structure de K-algèbre (K[X], +,x, .)une K algebre commutative 1 élément neutre
produit de polynôme:
∀n∈N, c_n =Σ a_kb_n−k (de k=0 a n)
= Σ a_kb_l (de k+l=n)
PPTE DE PRODUIT
Commutativité P×Q=Q×P.
Element neutre pour × : P ×1K[X] = 1K[X] ×P = P
Elément absorbant pour × : 0K[X] × P = P × 0K[X] = 0K[X].
Associativité et distributivité (gauche, droite)
X^(n+p) =X^n×X^p.
structure de K espace vecto
un K espace vecto de dim infinie
(K[X], +, x)
∀p ∈ N, [X^n]_p = δ_n,p. =1 si n=p
=0 sinon
famille {(Xn)n∈N} est une base de K[X]= base canonique
Si d est un entier naturel, l’ensemble des poly de deg d n’est pas un SSEV de K[X].
degré echelonne :
i) i∈[0,n] P_i est non nul
ii) pour tout i ∈ [0, n − 1], deg(P_i ) < deg(P_i+1)
suite (deg(P_i))_i∈[0,n] est strictement croissante
Indépendance linéaire des familles de poly de degré échelonné
Toute famille de poly de degré échelonné de K[X] est une famille libre de K[X]
PPTE SUR LE DEGRE
deg(P+Q) <= max(deg(P),deg(Q))
si poly ≠0 et deg different alors on a égalité
deg(P × Q) = deg(P) + deg(Q).
deg(λP) = −∞ si λ = 0
=deg(P) si λ≠0
si P=0 alors deg(P)=-inf
ensemble K_n[X]
poly à coefficients dans K deg <=n
un K espace vecto de dim finie
un SSEV de K[X]
(1, X , . . . , X_n ) est une base canonique.
dim(K_n [X ]) = n + 1
ensemble K[X]
K[X] l’ensemble des poly à coefficients dans K
P=(a_n) une suite presque nulle
∃n0 ∈N, ∀n∈N, n>= n0, a_n =0.
deg(P) = max{n ∈ N : a_n≠ 0}
P=(1,0,0,3,2,0,6,0...0)--> degP=6 mais cd(P)=6
coef dominant monôme de plus haut degré
1=X_0 = (1,0,...), X_1 = (0,1,0,...)=X
X_n est la suite dont les termes sont nuls
sauf celui d’indice n + 1 qui vaut 1.
P = (a_n), on pose
P=Σ a_n*X^n (nb fini de terme comme (an) s'annule)
application injective
ARITHMETIQUE
FACTORISATION DE
POLYNOMES
polynômes irréductibles:
a) P ∉ K_0 [X] P est non constant
b) ∀(P_1,P_2) ∈K[X],
(P=P_1*P_2 ⇒P_1 ∈K_0[X]ouP_2 ∈K_0[X]).
Caractérisation des polynômes irréductibles.
1. Les polynômes irréductibles de C[X] sont les polynômes de degré 1
tt poly non cst est divisible par au moins un poly irréductible
2. Les polynômes irréductibles de R[X] sont
• les polynômes de degré 1 ;
• les polynômes de degré 2 dont le discriminant est strictement négatif.
Décomposition en produits de facteurs irréductibles.
des entiers naturels non nuls α1, . . . , αn
des polynômes P1, . . . , Pn irréductibles dans K[X] tels que
P = ∏ P_k ^(α_k) (de k=1 à n)
décomposition est unique à permutation près et à multiplication par scalaire près.
polynôme scindés
produit de polynômes de degré 1,
P = ∏ P_k (de n=1 à k)
P=P_1*P_2...P_n
Relation entre coefficients et racines.
P scindé sur K et on pose n = degP.
a_0,...,a_n les coefficients de P dans la base canonique de Kn[X]
x_1, . . . , x_n les racines de P dans K
P= ∑a_p*X^p = a_n∏(X−x_j).
somme de p=0 à n, produit de j=1 à n
1. Somme des racines deP: ∑x_j =−( a_(n-1)) / a_n ·
2. Produit des racines de P:∏x_j = (-1)^n *a_0 / a_n
Théorème de D’Alembert-Gauss.
polynôme non constant de C[X] scindé dans C.
polynôme non constant de C[X] admet au moins une racine dans C.
décomposition ou les racines sont réels
alors scindé dans R
tt poly est scindé dans C
Tout polynôme P de K[X] scindé sur K admet:
un degré et deg(P)≥ 1.
au moins une racine dans K
tt polynômes de deg n admet
exactement n racines dans C
racine multiple a est une racine d’ordre m de P si
• j dans [[0,m−1]], P(j)(a)=0_K;
• P^(m)(a)≠ 0_K. m la multiplicité de la racine a dans P
i) a est racine d’ordre au moins m de P ;
ii) (X − a)^m divise P .
Caractérisation des racines multiples par divisibilité.
LASSE
i) a est racine d’ordre m de P;
ii) (X − a)^m divise P et (X − a)^(m+1) ne divise pas P.
racine de polynômes
a est une racine de P si P(a) = 0_K
infinité de racines dans K, alors P = 0K[X].
Majoration du nombre de racines d’un polynôme non nul.
Le nombre de racines de P est inférieur ou égal à deg P.
α_k est une racine de P,
alors ∏(X − α_k) divise P =>α_k deux à deux distincts
k dans [[1, n]]
LASSE
a est racine de P;
(X−a) divise P
division euclidienne
A=BQ+R et(R=0_K[X] ou deg(R)
divisibilité dans K[X]
On dit que B divise A dans K[X] A = BQ.
deg(B)<=deg(A)