Quadratic Equations By. Eshal Khaliq

更多类似内容

unit 2

由Kassandra Perez

Quadratic Equations

由stefn dreaves

Vertex Form

由DANIEL SHANG

Exponets

由Kaur Ishkeerat

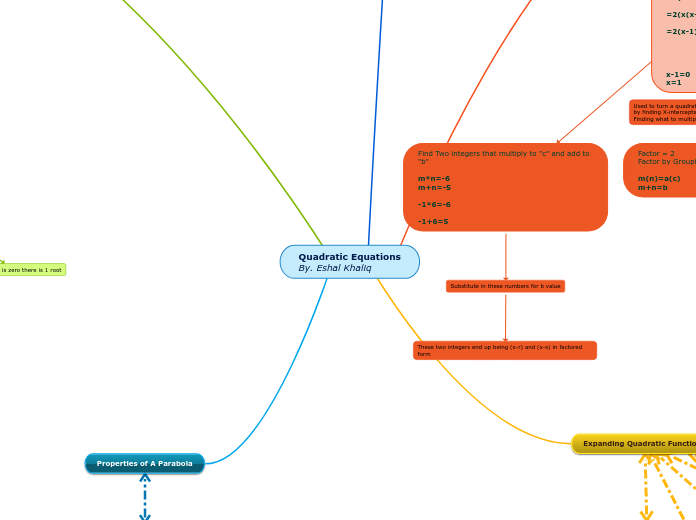
Trinomial Standard Form ax^2+bx+c ---------------------------- 2x^2+10x-12 =2(x^2+5x-6) =2(x^2-1x+6x-6) =2(x(x-1)+ 6(x-1) =2(x-1)(x+6) x-1=0 x+6=0 x=1 x=-6

If the trinominal cannot be common factored and the a value is more than 1, you have to multiply a and c

Factor = 2 Factor by Grouping (not always necessary) m(n)=a(c) m+n=b

Find Two integers that multiply to "c" and add to "b" m*n=-6 m+n=-5 -1*6=-6 -1+6=5

Substitute in these numbers for b value

These two integers end up being (x-r) and (x-s) in factored form

Quadratic Equations By. Eshal Khaliq

Properties of A Parabola

Parabola

Optimum Value

The highest or lowest point on a parabola. If the parabola goes downwards it's maximum, and if it's going upwards it's minimum.

Vertex

The point where the axis of symmetry and the parabola meet at it's maximum or minimum value.

Axis of Symmetry

Is a vertical line that divides the parabola into two equal parts. The axis of symmetry is the sum of the roots divided by two.

Zeros

Also called roots. They are the x-intercepts of a parabola, and can have one, two, or zero roots.

Y- Intercept

The co-ordinate where the parabola crosses the y-axis.

Solving Quadratic Equations

Quadratic Equation

Finding x-intercepts from Standard Form using Quadratic Formula X-intercepts/Roots/Zeroes = Solutions

(b^2-4ac)

Discriminant

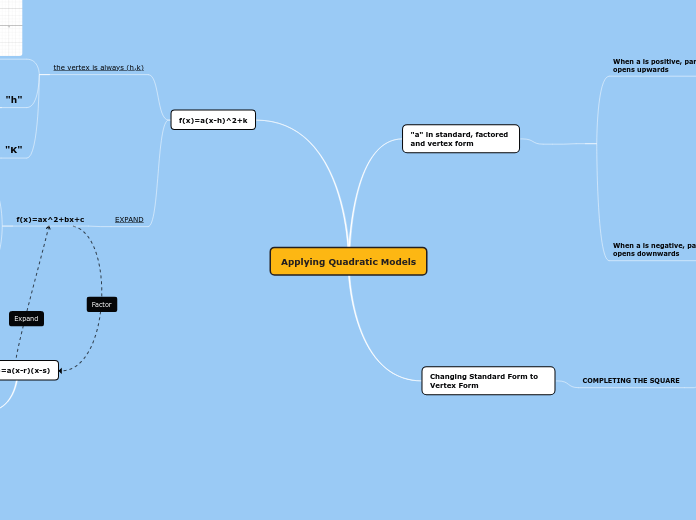
Completing the Square

Convert Standard Form to Vertex Form and find Maximum/Minimum values or vertex of parabolas

ax^2 + bx + c = a(x-h)^2 + k

y=3x^2-12x-5 y=(3x^2-12x)-5 y=3(x^2-4x)-5 -4/2=-2^2=4 y=3(x^2-4x+4)-5 y=3(x^2-4x+4)-17 y=3(x-2)^2-17

Put brackets around ax^2+bx terms Common Factor the "a" value Make Perfect Square Trinomial inside bracket using: (b/2)^2 Add the opposite sign of the (b/2)^2 inside the bracket EX. 2(x^2+6x+9-9)+11 Move the opposite sign (b/2)^2 value outside bracket by multiplying it by "a" value Add this value with the k value outside bracket to get final k value Keep the "a" value outside bracket and square root the first term x^2, keep the sign of the middle term (addition or subtraction) and square root the last term in bracket, add a square outside of end bracket to give you: (x-h)^2 Write out the final Equation that is left over Vertex = (2,17) Minimum = -17

Expanding Quadratic Functions

Distributive Property

a(b + c) = ab + ac Example 1

2(x + 4) = 2(x + 4) =2x+8 Example 2

Expanding Binomials

(a + b)(c + d) = ac + ad + bc + bd e.g. (x + 4)(x – 3) = x^2 – 3x + 4x – 12 = x^2 + x – 12 Example 1

Perfect Square Trinomials

4x^2+12x+9 4(9) = 36 m(n)=36 m = 6 n+n=12 n = 6 Substitute as bx term = 12x =4x^2+6x+6x+9 =2x(2x+3)+3(2x+3) =(2x+3)(2x+3) =(2x+3)^2 Example 2

Factor out the GCF by dividing it with all the terms Move GCF outside of bracket Multiply a value and c value Find two numbers that multiply to the product of a(c) and have the sum of b Substitute the two numbers for the middle term Group the terms with common factors and factor each binomial group The last two binomials should be the same so you simplify them together by writing the product as the square of the binomial

(2x – 3)(2x – 3) = (2x – 3)^2

Same method of factoring is used as factoring trinomials except you write the product as the square of a binomial Example 1

a^2±2ab+b^2 = (a±b)^2 We have to find out what a and b are

2ab = 2(2x)(3) = 4x(3) = 12x

Therefore, 2ab is the middle term which means it is a square trinomial

a^2 = 4x^2 so a=√4x^2 = 2x b^2 = 9 so b=√9 = 3

Difference of Squares

( x + a ) ( x - a ) = x^2 - 5x + 5x -25 = x^2 -25 The middle terms cancel out Example

Foil Method

First Outside Inside Last ( x + 3 ) (x + 2 ) = x^2 + 2x + 3x + 6 = x^2 + 5x + 6

Example 1

Example 2

Factoring

Used to turn a quadratic into factored form to solve equation by finding X-intercepts Finding what to multiply together to get an expression

Forms of Quadratic Equations

Square Roots

Vertex Form

y = a(x-h)^2 + k

Vertex (h,k) k = y value of the vertex "k" represents a vertical shift h = x value of the vertex and axis of symmetry

"h" represents a horizontal shift

"k" represents a vertical shift

Factored Form

y = a(x-r)(x-s)

If a > 1 or a < -1, then the graph is stretched vertically by a factor of a a = vertical stretch/compression factor

a = vertical stretch/compression factor

Use Step Pattern for plotting points of parabola

Step Pattern -------------- a=2 2, 6, 10, 14,....

Step Pattern -------------- a=1 1,3,5,7,9,....

Standard Form

y = ax^2 + bx + c

a value cannot be 0 x is the unknown variable a, b and c are all known values c value is the y-intercept of parabola a = vertical stretch factor

Discriminant Form

b²-4ac

If discriminant is zero there is 1 root

Positive discriminant = 2 roots

Negative discriminant = no real roots