Global Citizenship
Issues
Religious persecution
Moral deterioration
Selfishness
Cultural colonization
Financial Meltdown
Aggressive nationalism
Global instability
Climate crisis
Threat of arificial intelligence
Geopolitical tensions
Divisions, Inequalities, Challenges
Negativity towards communities/societies
Aspects
Bonding
Culture of encounter
Freedom
Democracy
Fraternal Openness
Mechanisms of dialogue/mediation
Protection of human rights
Collective problem solving
International cooperation
Influence in behaviour
Ideas become concepts
Importance of taking action
Técnicas para hablar fluido y claro
5. Preparar guiones
4. Respirar, serenarse
3. Elaborar listas de palabras y sus sinónimos
2. Informarse del tema
1. Identificar el origen de mis defectos
10. Leer un texto con un lápiz en la boca para mejorar la dicción.
9. Pausas después de cada frase
8. Buscar retroalimentación para identificar muletillas en mi forma de hablar
7. Pensar antes de hablar
6. Terminar una idea antes de comenzar otra nueva
S.E.L HOMOGÉNEOS: son aquellos sistemas que tienen la forma matricial AX=0.
Solución No Trivial: sistema en el que no todos los valores de las incógnitas es 0.
Solución Trivial: es aquella que sin resolver el sistema sabemos su resultado.
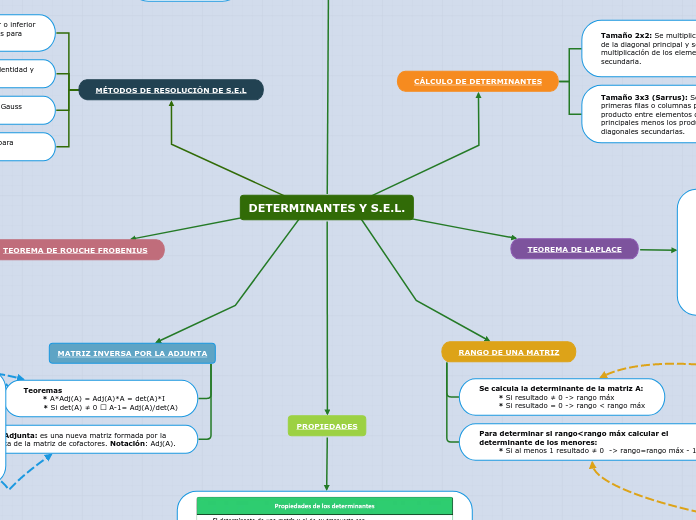
DETERMINANTES Y S.E.L.
MÉTODOS DE RESOLUCIÓN DE S.E.L
4. Crammer: Utiliza determinantes para hallar cada incógnita.
3. Matriz Inversa (X=A-1*b): 3.1 Gauss Jordan 3.2 Matriz Adjunta
2. Gauss-Jordan: forma la matriz identidad y se tiene los valores de cada incógnita.
1. Gauss: forma una matriz superior o inferior de la matriz ampliada, forma ecuaciones para encontrar incógnitas.
TEOREMA DE ROUCHE FROBENIUS
* Solución única: Rango(A) = Rango(A|b) = # incógnitas
* ∞ soluciones: Rango(A) = Rango(A|b) ≠ # incógnitas
* Sin solución: Rango(A) ≠ Rango(A|b) y Rango(A) < Rango(A|b)
MATRIZ INVERSA POR LA ADJUNTA
Matriz Adjunta: es una nueva matriz formada por la transpuesta de la matriz de cofactores. Notación: Adj(A).
Teoremas
* A*Adj(A) = Adj(A)*A = det(A)*I
* Si det(A) ≠ 0 A-1= Adj(A)/det(A)
RANGO DE UNA MATRIZ
Para determinar si rango rango=rango máx - 1
Se calcula la determinante de la matriz A:
* Si resultado ≠ 0 -> rango máx
* Si resultado = 0 -> rango < rango máx
TEOREMA DE LAPLACE
Desarrollo de Cofactores: Se escoge una columna o fila y multiplicamos cada elemento de la misma por el cofactor correspondiente (Aij) que se determina Cij=(–1)i+j*det(Mij).
PROPIEDADES
CÁLCULO DE DETERMINANTES
Tamaño 3x3 (Sarrus): Se aumentan las dos primeras filas o columnas para realizar el producto entre elementos de las tres diagonales principales menos los productos de las tres diagonales secundarias.
Tamaño 2x2: Se multiplica entre los elementos de la diagonal principal y se resta la multiplicación de los elementos de la diagonal secundaria.
DEFINICIONES
Menores
Submatriz Mij de tamaño (n-1) que resulta al eliminar la fila i y la columna j del elemento aij de una matriz A.
Determinante
Sea A=aij una matriz de tamaño n*n, det(A) se define mediante una sumatoria que involucra todas las permutaciones.
Inversión
Se da cuando en una permutación hay un entero mayor jr que precede a uno menor js.
Permutación
Pares e Impares
Si # de inversiones es impar: permutación impar y (-)
Si # de inversiones es par: permutación par y (+)
Reordenamiento de los elementos de un conjunto S={1,2,3,…n} formado por números enteros ascendentes de 1 a n de forma {j1,j2,j3,…jn}.