DISTRIBUCIONES DE PROBABILIDAD

Mere som dette

DISTRIBUCIÓN DE LA PROBABILIDAD.

af luis reyes matias

Estadística descriptiva y probabilidad

af Brayan Camilo Roa

Falacias y tipos de falacias

af Esteban Jaramillo

Probabilidad: Conceptos básicos

af Javier González

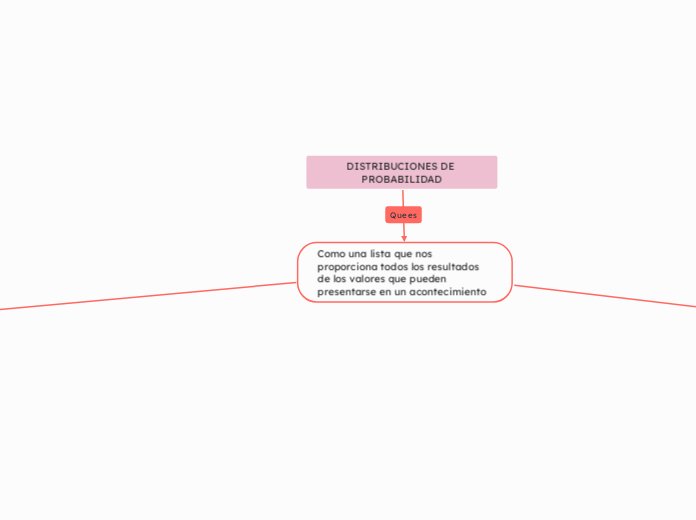
DISTRIBUCIONES DE PROBABILIDAD

Como una lista que nos proporciona todos los resultados de los valores que pueden presentarse en un acontecimiento

DISCRETAS

Las distribuciones de probabilidad continuas, como la distribución normal, describen valores en un rango o escala y se muestran como figuras sólidas en la galería de distribuciones. Las distribuciones continuas son en realidad abstracciones matemáticas, ya que suponen la existencia de cada valor intermedio posible entre dos números. Es decir, una distribución continua asume que hay un número infinito de valores entre dos puntos de la distribución.

BIMONIAL ACUMULADA

la función de distribución acumulativa de una variable aleatoria binomial, la cual nos permite resolver de manera rápida muchos problemas de distribución binomial

Para calcular las probabilidades acumuladas existen 2 opciones

Calcular cada probabilidad de forma individual.

Usar la tabla de probabilidades acumuladas

Una moneda cuenta con 2 caras: gato y perro. Si se lanza 4 veces la moneda, calcular la probabilidad de obtener 2 o menos perros.

un ensayo consiste en lanzar una moneda. Vamos a considerar un éxito si obtenemos un perro, caso contrario, consideraremos un fracaso si obtenemos un gato. El experimento binomial consta de una secuencia de 4 ensayos de estos, pues la moneda se lanza 4 veces. También sabemos que la probabilidad de obtener un éxito (perro) al lanzar una moneda es de 50 % o 0,5.

HIPERGEOMETRICA

La distribución hipergeométrica es especialmente útil en todos aquellos casos en los que se extraigan muestras o se realicen experiencias repetidas sin devolución del elemento extraído o sin retornar a la situación experimental inicial. Es una distribución fundamental en el estudio de muestras pequeñas de poblaciones pequeñas y en el cálculo de probabilidades de juegos de azar. Tiene grandes aplicaciones en el control de calidad para procesos experimentales en los que no es posible retornar a la situación de partida.

- "n" pruebas, separadas o separables de entre un conjunto de "N" pruebas posibles. -Cada una de las pruebas puede dar únicamente dos resultados mutuamente excluyentes. -El número de individuos que presentan la característica A (éxito) es "k". -En la primera prueba las probabilidades son: P(A)= p y P(A)= q; con p+q=1.

Formula y ejemplo

DISTRIBUCIÓN DE POISSON

Sus principales aplicaciones hacen referencia a la modelización de situaciones en las que nos interesa determinar el número de hechos de cierto tipo que se pueden producir en un intervalo de tiempo o de espacio, bajo presupuestos de aleatoriedad y ciertas circunstancias restrictivas.

· Se observa la realización de hechos de cierto tipo durante un cierto periodo de tiempo o a lo largo de un espacio de observación · Los hechos a observar tienen naturaleza aleatoria ; pueden producirse o no de una manera no determinística. · La probabilidad de que se produzcan un número x de éxitos en un intervalo de amplitud t no depende del origen del intervalo (Aunque, sí de su amplitud) · La probabilidad de que ocurra un hecho en un intervalo infinitésimo es prácticamente proporcional a la amplitud del intervalo. · La probabilidad de que se produzcan 2 o más hechos en un intervalo infinitésimo es un infinitésimo de orden superior a dos.

BIMONIAL

La distribución binomial es una distribución de probabilidad discreta que nos dice el porcentaje en que es probable obtener un resultado entre dos posibles al realizar un número x de pruebas. La probabilidad de cada posibilidad no puede ser más grande que 1 y no puede ser negativa.

si lanzamos un dado la posibilidad de que el resultado sea par (2, 4 ó 6) o impar (1, 3 ó 5) será exactamente la misma si el dado está bien equilibrado, el 50% y por muchas veces que lo lancemos la probabilidad, en cada una de esas veces, seguirá siendo el 50%.

En estas pruebas deberemos tener sólo dos resultados posibles, como al lanzar una moneda que salga cara o cruz o en una ruleta francesa que salga rojo o negro.

CONTINUAS

Las distribuciones de probabilidad discretas describen valores distintos, normalmente números enteros, sin valores intermedios, y se muestran como una serie de columnas verticales, como la distribución binomial en la parte inferior del cuadro de diálogo

DISTRIBUCION EXPONENCIAL

La distribución exponencial a menudo se refiere a la cantidad de tiempo hasta que ocurre algún evento específico. Por ejemplo, la cantidad de tiempo (comenzando ahora) hasta que ocurra un sismo tiene una distribución exponencial. Otros ejemplos incluyen el tiempo, en minutos, de las llamadas telefónicas de negocios de larga distancia, y la cantidad de tiempo, en meses, que dura la batería de un automóvil. Se puede demostrar, también, que el valor del cambio que tienes en tu bolsillo o bolso aproximadamente sigue una distribución exponencial.

Ejemplo

DISTRIBUCION UNIFORME

Parametros

La distribución o modelo uniforme puede considerarse como proveniente de un proceso de extracción aleatoria .El planteamiento radica en el hecho de que la probabilidad se distribuye uniformemente a lo largo de un intervalo

Formula