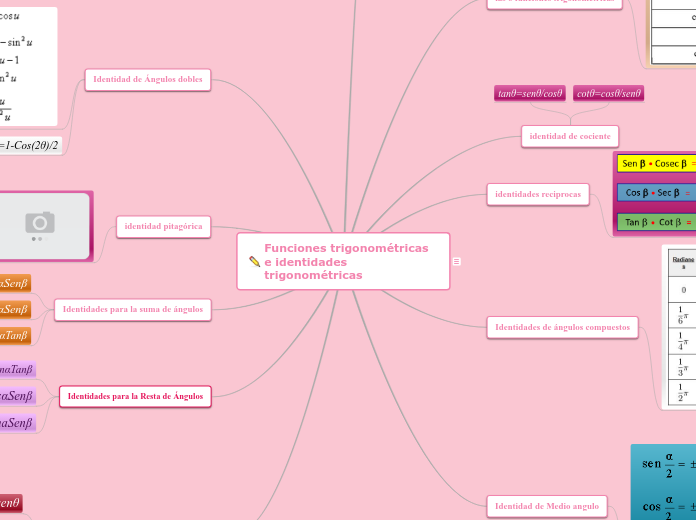
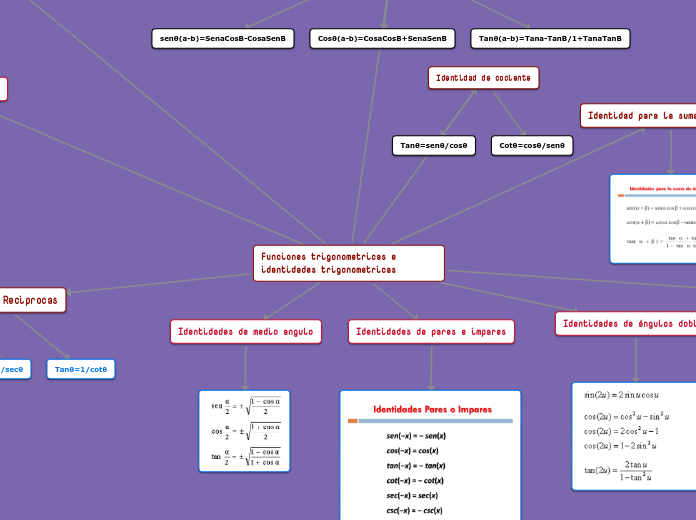
Funciones trigonométricas e identidades trigonométricas
las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razanoes trigonometricas a todos los números reales y complejos y Una identidad trigonométrica es una igualdad que vincula dos
funciones trigonometricas y es válida en el dominio común o descartando los puntos que anulan alguna función en caso de ser divisor.
Identidades trigonométricas pares e impares
Tan(-θ)=-CO/CA=-Tanθ
Cot(-θ)=CA/-CO=-cotθ
cos(-θ)=CA/H=cosθ
sec(-θ)=H/CA=secθ
sen(-θ)=-CO/H=-senθ
csc(-θ)=H/-CO=-cscθ
Identidades para la Resta de Ángulos
Cosθ(a-β)=CosaCosβ+SenaSenβ
Senθ(α-β)=SenαCosβ-CosαSenβ
Tanθ(α-β)=Tanα-Tanβ /1+TanαTanβ
Identidades para la suma de ángulos
Tanθ(α+β)=Tanα+Tanβ /1-TanαTanβ
Cos θ(α+β)=CosαCosβ+SenαSenβ
sen θ(α+β)=SenαCosβ+CosαSenβ
identidad pitagórica
Identidad de Ángulos dobles
sen^2=1-Cos(2θ)/2
Las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razanoes trigonometricas a todos los números reales y complejos y Una identidad trigonométrica es una igualdad que vincula dos
funciones trigonometricas y es válida en el dominio común o descartando los puntos que anulan alguna función en caso de ser divisor.
Teoremas de la suma y diferencia de ángulos[
Pueden demostrarse según la Fórmula de Euler o mediante la proyección de ángulos consecutivos. La identidad de la tangente surge del cociente entre coseno y seno, y las restantes de la recíproca correspondiente
Identidad de Medio angulo
Identidades de ángulos compuestos
identidades reciprocas
identidad de cociente
cotθ=cosθ/senθ
tanθ=senθ/cosθ
las 6 funciones trigonométricas