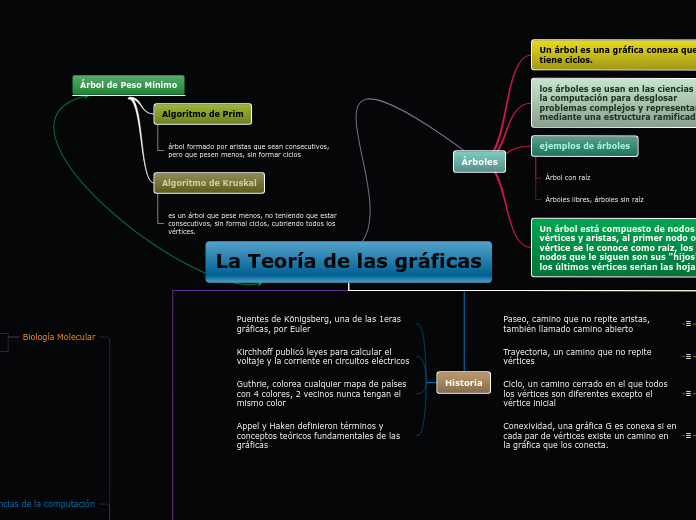
Árbol de Peso Mínimo
Algoritmo de Kruskal
es un árbol que pese menos, no teniendo que estar consecutivos, sin formal ciclos, cubriendo todos los vértices.
Algoritmo de Prim
árbol formado por aristas que sean consecutivos, pero que pesen menos, sin formar ciclos
Árboles
Un árbol está compuesto de nodos o vértices y aristas, al primer nodo o vértice se le conoce como raíz, los nodos que le siguen son sus "hijos" y los últimos vértices serían las hojas
ejemplos de árboles
Árboles libres, árboles sin raíz
Árbol con raíz
los árboles se usan en las ciencias de la computación para desglosar problemas complejos y representarlos mediante una estructura ramificada.
La reorientación del aparato estatal y de sus funciones, tales como el recorte en gastos gubernamentales para el bienestar social.
Un árbol es una gráfica conexa que no tiene ciclos.
La reprivatización de la economía (la venta de empresas estatales y paraestatales, incluyendo la recién nacionalizada banca).
La Teoría de las gráficas
Grafos
G=(v,e) donde v significa vértices y la e es de (edges, en inglés) pero para nosotros serían las aristas
Grafos no dirigidos, no cuentan con una dirección en específico
Grafos dirigidos, donde se puede ir de A a B, pero de B a A no se puede
Multigrafos, donde existen varios caminos entre vértices
Gafos ponderados, donde las aristas ya tienen valores
Grafos simples, con vértices y aristas solamente
Caminos
Conexividad, una gráfica G es conexa si en cada par de vértices existe un camino en la gráfica que los conecta.
Control de Salario
Ciclo, un camino cerrado en el que todos los vértices son diferentes excepto el vértice inicial
Aperturas de Mercado Interno
Trayectoria, un camino que no repite vértices
Políticas de Reformas de Estado
Paseo, camino que no repite aristas, también llamado camino abierto
Privatizaciones Masivas
Historia
Appel y Haken definieron términos y conceptos teóricos fundamentales de las gráficas
Guthrie, colorea cualquier mapa de países con 4 colores, 2 vecinos nunca tengan el mismo color
Kirchhoff publicó leyes para calcular el voltaje y la corriente en circuitos eléctricos
Puentes de Königsberg, una de las 1eras gráficas, por Euler
Aplicaciones en la actualidad
Área didáctica y lúdica
creación de laberintos con una estrecha relación entre la teoría de gráficas y la papiroflexia
permite modelar y resolver juegos como el dominó, el juego Nim, come-solo, Torres de Hanoi
Química
modelado de las partículas de carbono
Empresas dejándolas a la libre de fuerza de Mercado
fullerenos
Vender las empresas del Estado a la Iniciativa Privada, sin regular actividades económicas
matemáticas y ciencias de la computación
estudio de las redes sociales, almacenamiento de datos en servidores
la escritura de compiladores y la encriptación
recuperación de información
gráficos por computadora
lenguajes formales
sistemas operativos
construcción de robots basados en teoría de gráficas, álgebra lineal, estadística y geometría
diseño lógico, inteligencia artificial
generar nuevos algoritmos que efectúen simulaciones eficientes y que resuelvan problemas
Biología Molecular
mapas genómicos
modelos de proteínas