af Cristian Steven Perez Herrera 4 år siden
244
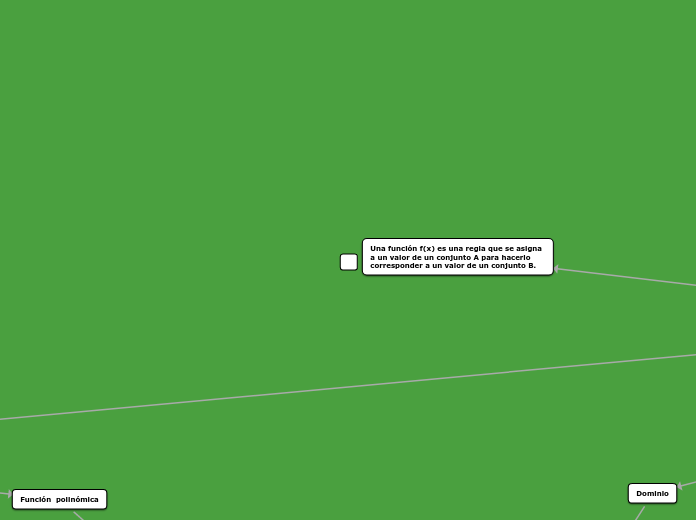
tarea relaciones y funciones
En matemáticas, las funciones pueden ser clasificadas según su comportamiento y características específicas, incluyendo su crecimiento o decrecimiento dentro de ciertos intervalos. Las funciones decrecientes disminuyen o se mantienen constantes, mientras que las continuas no presentan interrupciones en su gráfico.