af Yeisson Miranda 2 år siden
225
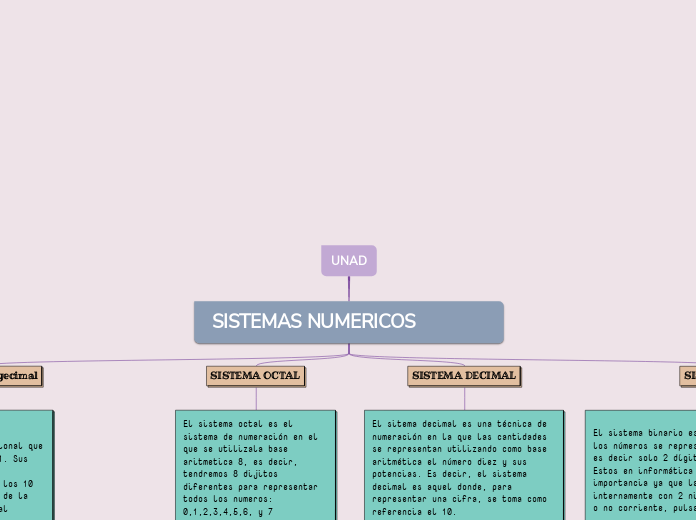
UNAD
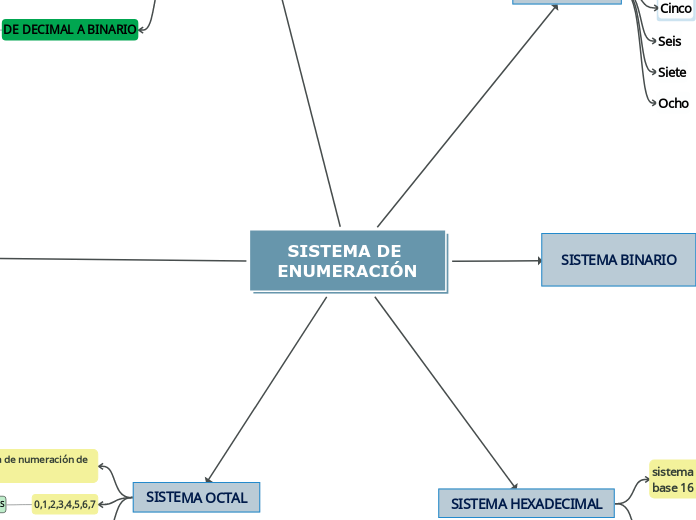
Los sistemas de numeración son fundamentales en la representación de cantidades y en el procesamiento de datos en la informática. Entre los más importantes se encuentran el sistema decimal, el sistema binario, el sistema hexadecimal y el sistema octal.