von Alanis Monroy Vor 3 Jahren
654
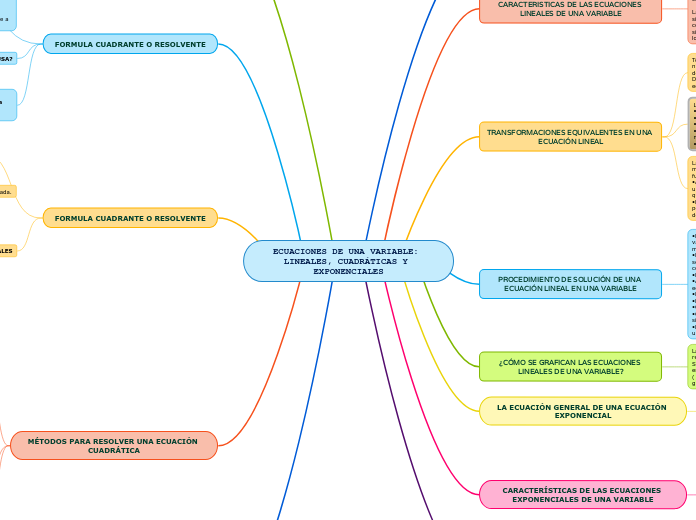
ECUACIONES DE UNA VARIABLE: LINEALES, CUADRÁTICAS Y EXPONENCIALES
Las ecuaciones de una variable pueden ser lineales, cuadráticas o exponenciales. Las ecuaciones lineales son aquellas en las que las variables están elevadas a la primera potencia y se pueden representar gráficamente como rectas en el sistema cartesiano.