Funzione

Mehr dazu

Diritto Schema.Mappa

von Andrea Nerozzi

Funzioni Reali

von Paola Rus

MOD.A.01.03.01 - Struttura organizzativa

von Maria Constanza Segura

MAPPA CONCETTUALE 3D

von MAZZOTTA FRANCESCO

Funzione

Nome: Eugerd
Cognome: Canaj
Classe: 4S
Scuola: Ipsia Castigliano
Anno scolastico: 2015/2016

Intersezione con gli assi

Segno

Limiti

Punti di discontinuità

3°specie

2°specie

1°specie

Calcolo limiti

Forma indeterminata

Asintoto

Obliqui

Orizzontali

Verticali

Le funzioni si dividono in:

Dispari

Una funzione f(x) si dice dispari se per ogni x appartenente al dominio, f(-x) = -f(x). 
Il grafico della funzione è simmetrico rispetto all'origine.

Pari

Una funzione f(x) si dice pari se per ogni elemento di X appartenente al dominio, 
f(-x) = f(x). Il grafico della funzione è simmetrico rispetto all'asse y.

Biettive

Una funzione si dice biettiva quando è sia iniettiva che suriettiva, cioè quando ad un solo elemento dell'insieme A corrisponde uno ed un solo elemento dell'insieme B e viceversa.

Suriettive

Una funzione si dice suriettiva quando ogni elemento dell'insieme B è immagine di almeno un elemento dell'insieme A.

Iniettive

Una funzione si dice iniettiva quando ad elementi distinti dell'insieme A corrispondo elementi distinti dell'insieme B.

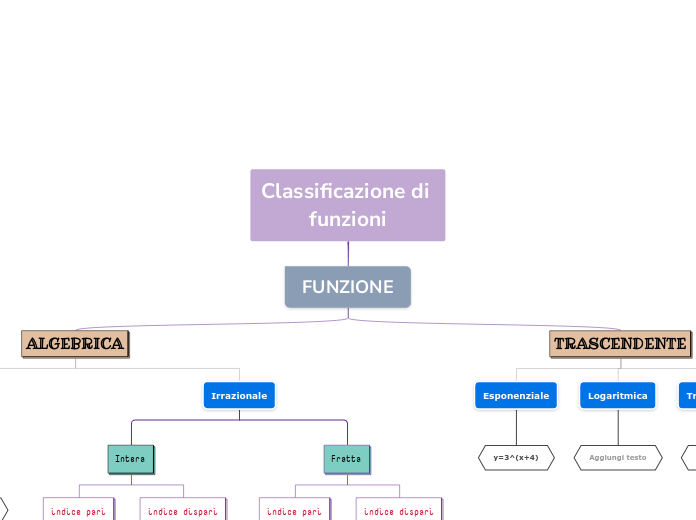
Tipologia

Algebriche

Razionali: -intere -fratte

Irrazionali: -intere -fratte

Trascendenti

In cui compaiono solo operazioni trascendenti: logaritmo, esponenziali, e funzioni goniometriche.

Codominio

Si dice codominio di una funzione f(y) l'insieme dei valori possibili che la variabile indipendente y può assumere, in modo che la funzione sia definita in tali valori.

Dominio

Il dominio di una funzione è il più ampio sottoinsieme di R costituito da tutti e soli i valori della X per cui esistano finiti i corrispondenti valori di Y=f(x)

Definizione

E' una relazione tra due insiemi A e B che associa ad un elemento X appartenente ad A uno e uno solo elemento Y appartenente a B.