von Jonathan Umaña R Vor 1 Jahr
71
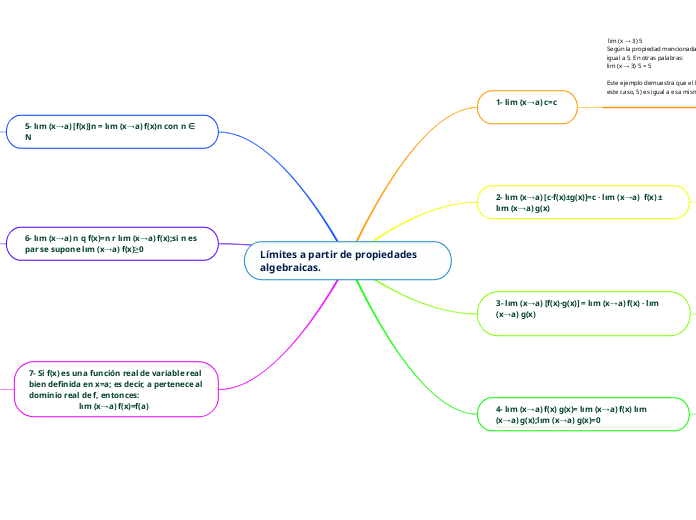
Límites a partir de propiedades algebraicas.
Las propiedades algebraicas de los límites permiten calcular el comportamiento de una función cuando la variable se aproxima a un punto específico dentro de su dominio. Si una función está bien definida en un punto, el límite de la función en ese punto es igual al valor de la función en ese mismo punto.