von simona santantonio Vor 5 Jahren
522
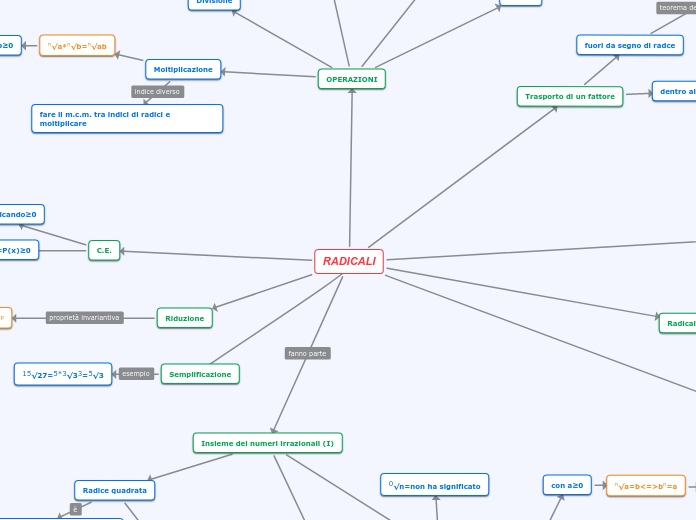
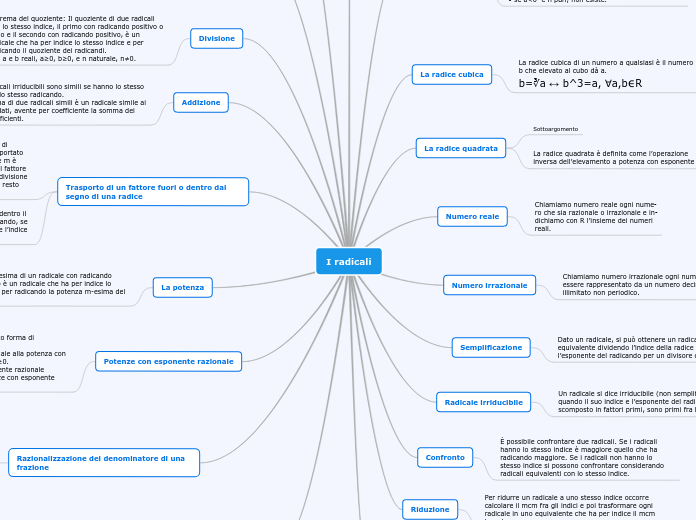
RADICALI
I numeri irrazionali, in particolare quelli rappresentati con radicali, giocano un ruolo significativo nelle operazioni matematiche. Le radici n-esime, come la radice quadrata e cubica, sono operazioni inverse dell’