RELACIÓN DE TAREAS, CRITERIOS Y CARACTERÍSTICAS
ACTIVIDAD 8: Ahora les toca a ellos. Para ello, completarán la actividad interactiva del REA y tras ello, expondrán el truco al resto de sus compañeros. Para ello, usarán Google Drive presentaciones para poder trabajar de forma colaborativa con sus compañeros.
ACTIVIDAD 8: Ahora les toca a ellos. Para ello, completarán la actividad interactiva del REA y tras ello, expondrán el truco al resto de sus compañeros. Para ello, usarán Google Drive presentaciones para poder trabajar de forma colaborativa con sus compañeros.
1 hora
Ordenador: Rea DUA y Google presentaciones
ACTIVIDAD 7:Analizarán paso a paso el truco que hemos visto en el video, respondiendo a las siguientes cuestiones:
- ¿Qué creéis que consigue el mago con este paso?
- Una vez que tenéis dos números que el mago os ha hecho creer que no tienen nada que ver, ¿Qué le va a pasar al resultado?
- Aunque parece magia, ¿Cuántas cifras del número hay que adivinar realmente?
- ¿Se te ocurre algún número para el que el truco no funcione?
ACTIVIDAD 7: Analizarán paso a paso el truco que hemos visto en el video, respondiendo a
las siguientes cuestiones:
- ¿Qué creéis que consigue el mago con este paso?
- Una vez que tenéis dos números que el mago os ha hecho creer que no tienen nada que ver, ¿Qué le va a pasar al resultado?
- Aunque parece magia, ¿Cuántas cifras del número hay que adivinar realmente?
- ¿Se te ocurre algún número para el que el truco no funcione?
Grupo de 3
ACTIVIDAD 6: Veremos un vídeo interactivo en el que nos enseñará un truco de magia utilizando el lenguaje algebráico y operaciones básicas con monomios . Además, comentaremos los videos que tienen en Symbaloo acerca de las operaciones básicas con monomios y ecuaciones de 1º grado.
ACTIVIDAD 6: Veremos un vídeo interactivo en el que nos enseñará un truco de magia utilizando el lenguaje algebráico y operaciones básicas con monomios . Además, comentaremos los videos que tienen en Symbaloo acerca de las operaciones básicas con monomios y ecuaciones de 1º grado.
ACTIVIDAD 5: Crearán una presentación con la ayuda de Canvas o Genially en el que aparecerá el algoritmo para la obtención de la letra final del DNI y la tabla que hace corresponder cada número con una letra. Además, tendrán que explicarlo con el número de su DNI y la letra.
Ordenador: Canvas o Genially
ACTIVIDAD 4: Realizarán un desafío cronometrado en el que tienen que averiguar que número del DNI es mayor, Retor o Cardia. Para ello, podrán acceder a la calculadora de letra de DNI que se le aporta en Symbaloo
ACTIVIDAD 4: Realizarán un desafío cronometrado en el que tienen que averiguar que número del DNI es mayor, Retor o Cardia. Para ello, podrán acceder a la calculadora de letra de DNI que se le aporta en Symbaloo
1.3.
1.3. Obtener las soluciones matemáticas en problemas de diversa complejidad, activando los conocimientos, utilizando las herramientas tecnológicas necesarias y, valorando e interpretando los resultados, aceptando el error como parte del proceso.
30 minutos
Ordenador: Symbaloo y Rea DUA
ACTIVIDAD 3: Completarán la actividad C del REA, que consiste en realizar la división de un DNI entre 23 y asociar el resto con una letra.
ACTIVIDAD 3: Completarán la actividad C del REA, que consiste en realizar la división de un DNI entre 23 y asociar el resto con una letra.
Ordenador: Rea DUA y calculadora
ACTIVIDAD 2: Tras la explicación, realizarán el ejercicio A y B: Números y
letras que consiste en completar una serie de palabras relacionadas con las características de un DNI explicado anteriormente
ACTIVIDAD 2: Tras la explicación, realizarán el ejercicio A y B: Números y
letras que consiste en completar una serie de palabras relacionadas con las características de un DNI explicado anteriormente.
Criterio de evaluación
1.2.
Aplicar, en problemas de la vida cotidiana y propios de las matemáticas, herramientas y estrategias apropiadas como pueden ser la analogía con otros problemas, la resolución de manera inversa (ir hacia atrás), la descomposición en problemas más sencillos, el tanteo, la estimación, el ensayo y error o la búsqueda de patrones, etc., que contribuyan a la resolución de problemas en situaciones de diversa complejidad.
Parejas
20 minutos
Ordenador: Rea DUA
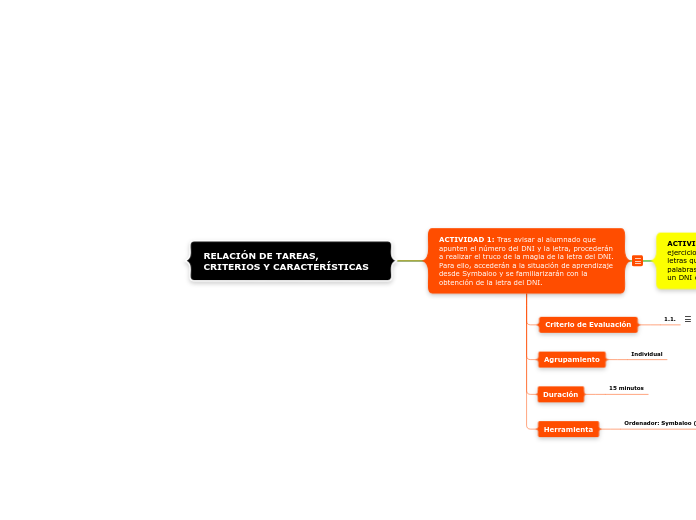
ACTIVIDAD 1: Tras avisar al alumnado que apunten el número del DNI y la letra, procederán a realizar el truco de la magia de la letra del DNI. Para ello, accederán a la situación de aprendizaje desde Symbaloo y se familiarizarán con la obtención de la letra del DNI.
Herramienta
Ordenador: Symbaloo (Videos)
Duración
15 minutos
Agrupamiento
Individual
Criterio de Evaluación
1.1.
1.1 Interpretar problemas matemáticos complejos, organizando y analizando los datos, estableciendo las relaciones entre ellos y comprendiendo las preguntas formuladas.