por Тамила Маллаева hace 5 años
342
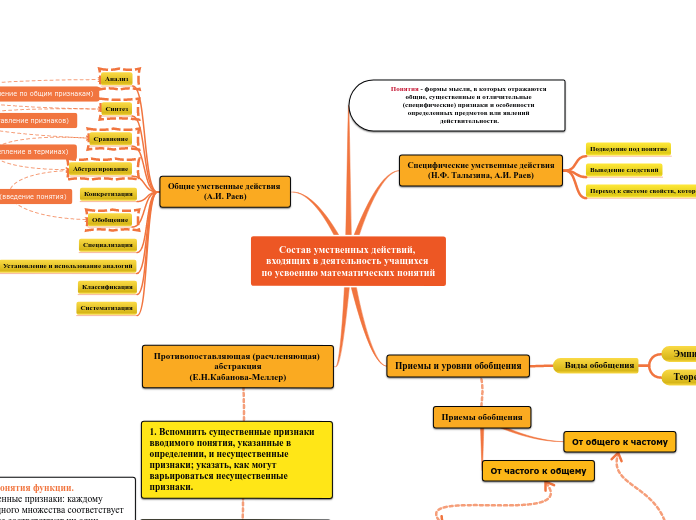
Состав умственных действий, входящих в деятельность учащихся по усвоению математических понятий
Введение новых понятий в математике включает в себя использование различных методов, таких как абстрактно-дедуктивный и конкретно-индуктивный. Абстрактно-дедуктивный метод предполагает нахождение существенных и несущественных признаков объектов, выделение объектов по этим признакам и их анализ.