Álgebra
Ecs lineales
Teo de Rouché-Frobenius
Cramer
Regla
Teo
Teo fundamental de equivalencia
Clasificación por coeficientes
General m≠n
Homogéneo b=0
Cuadrado o normal m=n
No homogéneo, b≠0
Homogéneo, si b=0
Forma matricial
A•X=B
Sistemas
Solución
Trivial
Compatible
Indeterminado
Determinado
Incompatible
Álgebra lineal
Mixto
Dependencia e independencia lineal
Base
Combinación lineal
Sistema generador
Dimensiones
Sp vectorial
Relaciones y funciones
Producto cartesiano (AxB)
Relaciones binarias
Simetría
Equivalencia
Reflexividad
Transitividad
Antisimetria
Composición
R^-1
Im R
Dom R
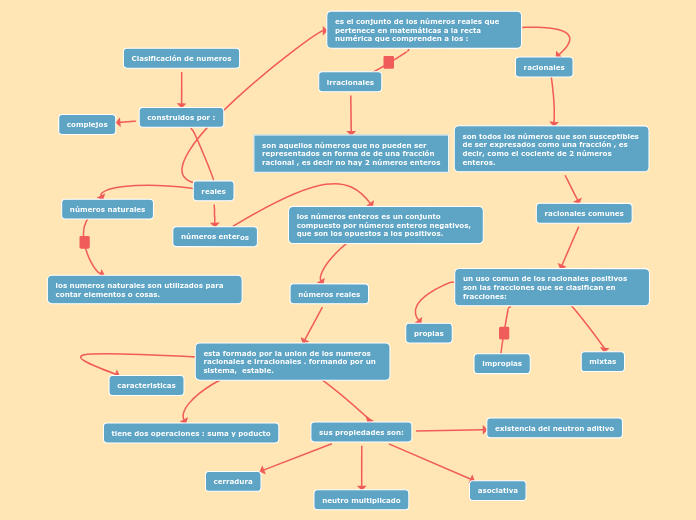
Conjs numéricos
Reales
Es cuerpo ordenado
Recta real
Amplitud
Valor absoluto
Complejos
Formas
Trigonometrica
Raíces de radiación
Representación
Exponencial
Par ordenado
Binomica
Conjugado
Es grupo abeliano
Algebraicamente cerrado
No ordenado
Potencias de i
Leyes de composición interna (+, •)
Racionales
Dominio de integridad
Potencia racional
Arquimedianidad
Completitud
Densidad
Enteros
Es anillo íntegro
Congruencia
Divisores impropios
No. primo
Teo fundamental de la aritmética
Potencia entera
Naturales
Es inductivo
(N, +,•) carece de estr
Principio de buena ordenación (BO)
Potencia natural
Operaciones inversas
Operaciones y propiedades
leyes
de Morgan
distributivas
diferencia simétrica
inverso
neutro
Resta
4 propiedades
Complemento
propiedades
A incluido B
involución
relación universal-vacío
Inclusión
antisimetría
transitividad
reflexividad
Unión
absorbente
neutro es vacío
conmutatividad
Intersección
absorbente es vacío
neutro es el universal
conmutividad
asociatividad
idempotencia
Matrices y determinantes
Tipos
(cuadrada, +,•)
Anillo conmutativo con unidad
Triangular
Antisimetrica
Simétrica
Unidad o identidad
Diagonal
Asociada a A
Conjugada
Traspuesta
Elementales
Matrices equivalentes
Forma escalonada
Potencia
Producto
Vectorial
Escalar
Suma vs diferencia
Geometría analítica
plano
ángulo entre ellos
d entre dos de ellos // no coincidentes
distancia entre punto y plano
determ por 3 puntos no alineados
recta
distancia entre punto y recta en el sp
dada por dos planos no //
simétrica
ángulo entre dos rectas
condiciones
perpendicularidad
paralelismo
por 2 puntos
dada por pendiente y punto
canónica
segmentaria
cartesiana
explícita
implícita
paramétrica
ec vectorial
Parábola
Hipérbole
Elipse
Círculo
Polinomios
Es dominio de integridad
Propiedades
Teo del resto
Raíz de P(x)
Relaciones entre raíces y coeficientes
Raíces múltiples
Raíces complejas
Teo de gauss
Teo fundamental de la descomposición factorial
Teo fundamental del álgebra
Fs polinomicas
producto
P(x)Q(x)=Σ[i=0;j=0→m+n](a↓j)(b↓k)x^i con j+k=i; gr(P+Q)= grP+grQ en un dominio de integridad, sino vale ≤
suma
sean los P: P(x), Q(x)€ A[x]/
gr(P+Q)≤máx{grP,grQ}
Q(x)= Σ[i=0→n](b↓i)x^i con (b↓n)≠0→grQ=n
P+Q= Σ[i=0→m]((a↓i)(b↓i)x^i
P(x)=Σ[i=0→m](a↓i)x^i con (a↓m)≠0→grP=m
Divisibilidad
Polis comprimos
Polinomio primo o irreducible
Teo fundamental de la aritmética K[x]
Relación de divisor
Teo de Ruffini
estructura de (A[x],+,•): dominio de integridad, anillo conmutativo con unidad; A[x] don't have divisores de cero
distributividad del producto respecto a la suma en A[x]:
₱P,Q€A[x]:(P+Q)R=PR+QR
E inversos multiplicativos en A[x]
esto no se cumple en A[x] pues no todo P(x)≠0 lo admite en él
inverso aditivo
Σ((a↓i)+(b↓i))x^i=Σ0x^i→(a↓i)+(b↓i)=0, ₱i→(b↓i)=-(a↓i)₱i→Q=Σ-(a↓i)x^i
neutro para •
(b↓i)=0,₱i≠0 (el polinomio unidad es de grado 0)
E neutro para +: (a↓i)+(b↓i)=(a↓i)₱i→(b↓i)=0→Q=Σ[i]0x^i
conmutatividad de + y•
asociatividad de + y •
es una expresión del tipo..., con todos los ai€A e i€N, x es un símbolo o indeterminada. a0 esa el término independiente y su an≠0, es el coeficiente principal
Igualdad
dos polinomios son= ←→ son del mismo grado y tienen =s coeficientes de las mismas potencias de x
Gr P(x)
grP= máx {i/ai≠0}
Combinatoria
Binomio de newton
Fórmula de Stieffel
Fórmula factorial
No. Combinatorio
Nos. De órdenes complementarios
(mn) =m!/n!(m-n)! =C
Casos particulares
Def
Nociones de lógica
Principios=leyes lógicas
Leyes de Morgan
Distributividad
Asociatividad
Conmutatividad
Idempotencia
Involución
Proposiciones
Clasificación
Contingencia
Contradicción
Tautologia
Funciones o esquemas
Circuitos lógicos
Cuantificadores
Universal
Existencial
Conectivos
Operaciones
Diferencia simétrica
entonces
Disyunción
Conjunciones
Negaciones