verdadero o verdadero es verdadero
verdadero o falso es verdadero
falso o verdadero es verdadero
falso o falso es falso
verdadero y verdadero es verdadero
verdadero y falso es falso
falso y verdadero es falso
falso y falso es falso
Estas reglas de De Morgan pueden generarse para cualquier número de variables
Subtema
(a+b)=ab
(ab)=a+b
Modelo lógico
Un juicio al cual se le aplica el operador lógico no (negación) forma un nuevo juicio.
Los valores que pueden asignarse a un juicio, desde el punto de vista lógico, son
dos: verdadero (V) o falso (F).
Si vinculamos los valores booleanos 0 y 1 con los valores lógicos F y V
respectivamente, encontramos que las operaciones del álgebra de Boole "binaria" asigna
correctamente los valores lógicos del juicio combinación.
Ley de De Morgan
Para todo par de elementos de G se cumple
Para cada elemento de G se cumple : a = |a
Para todo par de elementos de G se cumple :
a+ab=a
a(a+b)=a
ara todo par de elementos de G se cumple :
a+|ab= a+b
a(|a+b)=ab
Complemento de complemento
Propiedades
Neutros Cruzados
Para todo elemento en G se cumple
a+1=1
a*0=0
Demostración
a+1=a+(a+|a)
a+1=(a+a)+|a (asociativa)
a+1=a+|a (idempotencia)
a+1=1
a*0=0 (dualidad)
Asociativa
a) a (b c) (a b) c
b) a (b c) (a b) c
Idempotencia
Para todo elemento en G se cumple:
a+a=a
a*a=a
demostración
a+a=(a+a)
a+a=(a+a)*(a+|a)
a+a=a+(a*|a)
a+a=a+0
a+a=A
a*a=a (dualidad)
Dualidad
se presentan de a pares y en
tal forma que uno de la pareja se obtiene de otro cambiando "0" por "1" junto con "+" por ""
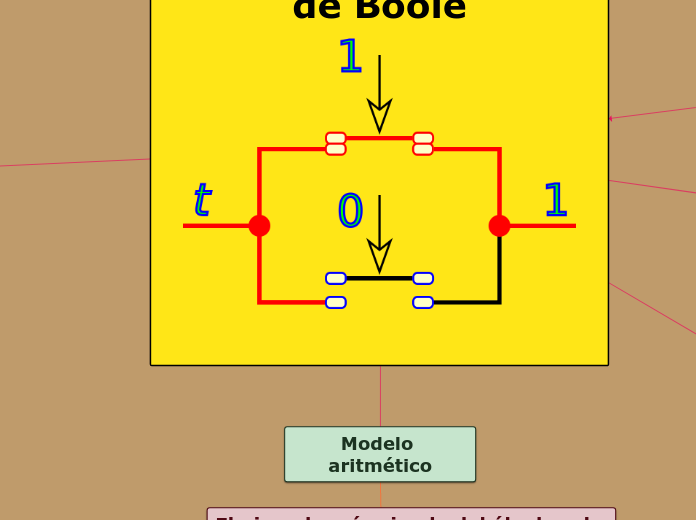
Modelo aritmético
El ejemplo más simple del álgebra de Boole se compone de un conjunto G de 2
elementos: "0" y "1".
Como es natural estos dos elementos deben coincidir con los neutros
de las reglas de combinación para satisfacer el axioma
Por lo tanto las reglas completas son:
1*1=1
1*0=0
0*1=0
0*0=0
1+1=1
1+0=1
0+1=1
0+0=0
Axiomas
Existen por lo menos dos elementos x, y en G tal que x <> y
Complemento
Para cada elemento a de G existe un elemento a tal que:
a*a=0
a+a=1
Distributivos
Para toda terna de elementos a, b, c pertenecientes a G se cumple:
a (a) a + (b c) = (a + b) (a + c)
b (b) a (b + c) = a . b + a c
Conmutativos.
Para todo par de elementos a y b pertenecientes a G se cumple:
(a) a + b = b + a
(b) a b = b a
Neutros
(b) Existe un elemento 1 en G tal que para cada a de G: a 1 = a
(a) Existe un elemento 0 en G tal que para cada a de G: a + 0 = a
(a) Se define una regla de combinación "+" en tal forma que a + b está en G siempre
que al menos a o b lo estén.
(b) Se define una regla de combinación "" en tal forma que a b está en G siempre
que tanto a como b lo estén.
Existe un conjunto G de objetos, sujetos a una relación de equivalencia, denotada
por "=" que satisface el principio de sustitución.
Esto significa que si a = b, b puede sustituir a a en cualquier expresión que la
contenga, sin alterar la validez de la expresión
Es una herramienta de fundamental importancia en el mundo de
la computación.
Las propiedades que se verifican en ella sirven de base al diseño y la
construcción de las computadoras que trabajan con objetos cuyos valores son discretos
Álgebra de Boole