por Neftalí Diaz hace 5 años
271
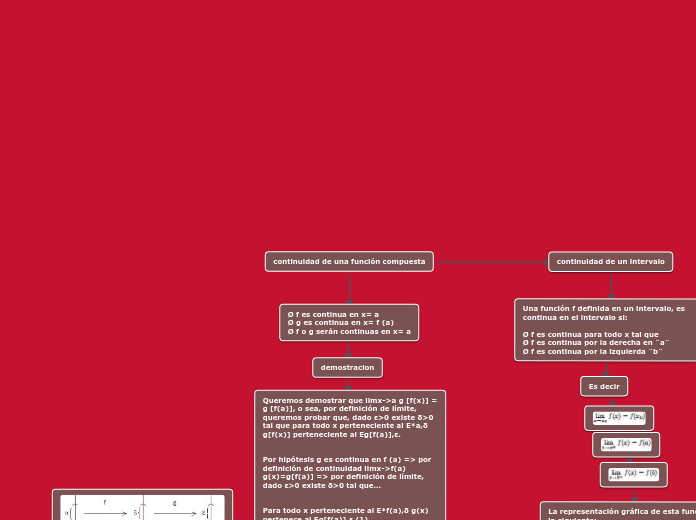
continuidad de una función compuesta
La continuidad de una función en un intervalo se define por su comportamiento en todos los puntos dentro de ese intervalo. Para que una función sea continua en un intervalo cerrado, debe ser continua tanto en el intervalo abierto como en los extremos del intervalo.