por Juleisy Cedeño hace 4 años
2254
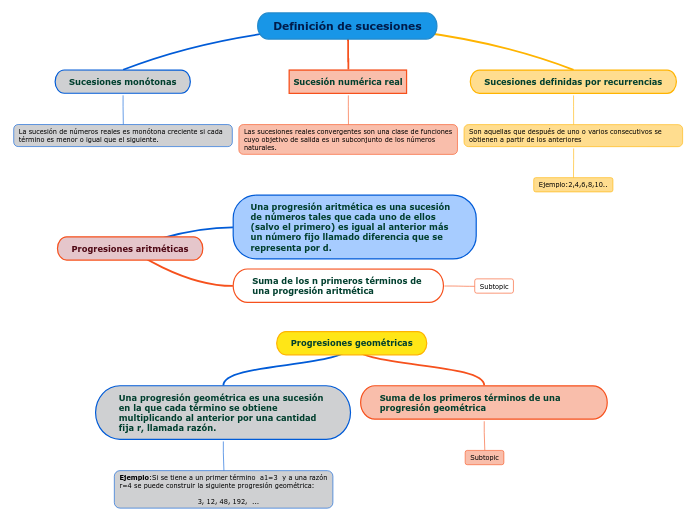
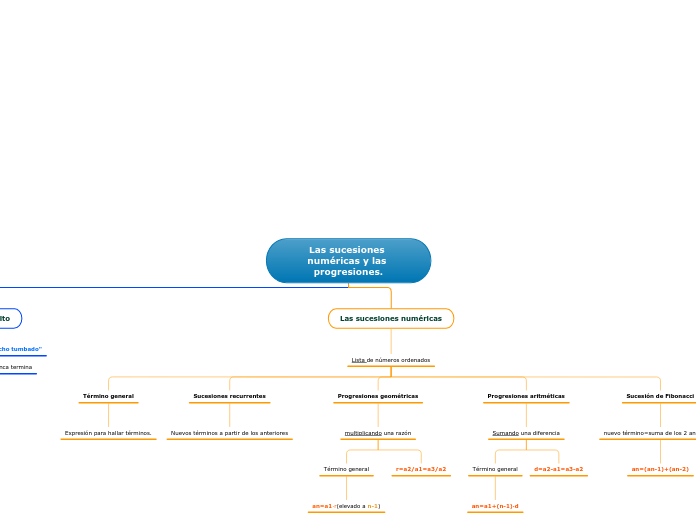
Definición de sucesiones
Las progresiones aritméticas y geométricas son tipos de sucesiones numéricas que se caracterizan por tener un patrón específico en la formación de sus términos. En una progresión aritmética, cada término se obtiene sumando una constante fija al término anterior, mientras que en una progresión geométrica, cada término se obtiene multiplicando el término anterior por una constante fija.