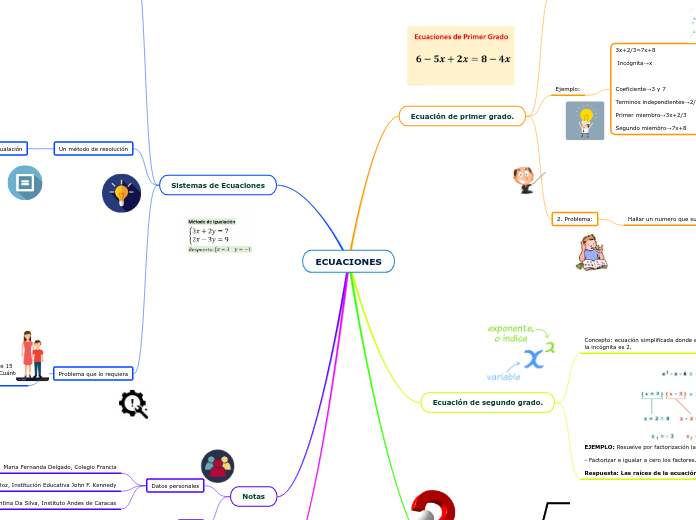
ECUACIONES
Referencias
Hoffmann, J. (2009). Selección de Temas de Matemática. Venezuela: Sphinx
Baldor, A. (2011). Álgebra (4ta reimpresión). México: Editorial Patria
Baldor, A. (1995). Álgebra (13a. ed.). México: Publicaciones Cultural
Notas
Fecha
30 de agosto de 2020
Datos personales
Valentina Da Silva, Instituto Andes de Caracas
Geraldson de la Hoz, Institución Educativa John F. Kennedy
Maria Fernanda Delgado, Colegio Francia
Sistemas de Ecuaciones
Problema que lo requiera
Ana tiene el triple de edad que su hijo Jaime. Dentro de 15 años, la edad de Ana será el doble que la de su hijo. ¿Cuántos años más que Jaime tiene su madre?
Respuesta: Ana tiene 45 años y su hijo Jaime 15, por tanto, Ana tiene 30 años más que su hijo.
Sistema de Ecuaciones
Resolución por el método de igualación
3j+15=2j+30
j=15
a=3(15)
a=45
a = edad de Ana
j = edad de Jaime
La edad de Ana es el triple que la de Jaime:
a = 3j
Dentro de 15 años, la edad de Ana será el doble que la de Jaime:
( a + 15 ) = 2( j + 15 )
Un método de resolución
Igualación
Ejemplo
Resolver el sistema
Pasos
5. La solución del sistema
4. Se sustituye el valor de la incógnita en una ecuación anterior.
2. Igualar entre sí los valores de la variable y resolver la ecuación.
1. Despejar una incógnita en ambas ecuaciones.
Explicación
Consiste en despejar la misma variable en ambas ecuaciones e igualar los valores obtenidos.
Concepto:
Dos o más ecuaciones
con varias variables
EJEMPLO
tienen una solución común
Problema
Si una raíz de la ecuación x² – (m + 1)x – 5 = 0 es 2, hallar la otra raíz.
Factorizando:
(2x + 5)(x – 2) = 0
⇒ x = -5/2
Sustituyendo valores:
∴ La otra raíz de la ecuación es -5/2
La ecuación cuadrática será:
x2 – (-3/2 + 1)x – 5 = 0
⇒ x2 + x – 10 = 0
Satisfacer la ecuación,
reemplazando:
⇒ 22 – (m + 1).2 – 5 = 0
⇒ 4 – 2m – 2 – 5 = 0 ⇒ m = -3/2.
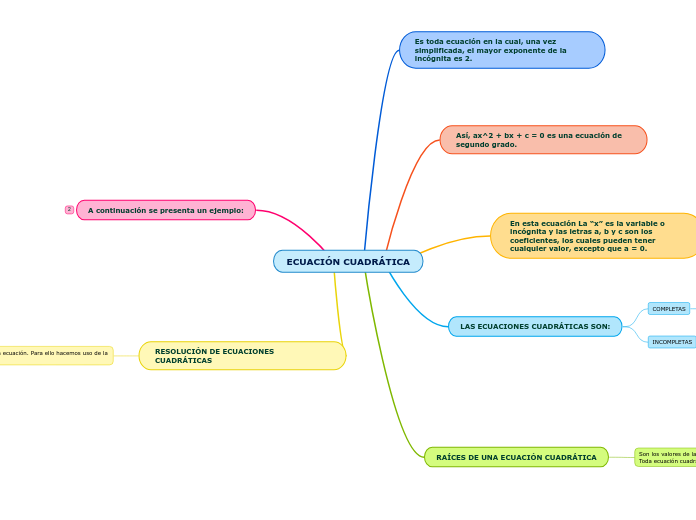
Ecuación de segundo grado.
EJEMPLO: Resuelve por factorización la ecuación x2 - x - 6 = 0
- Factorizar e igualar a cero los factores.
Respuesta: Las raíces de la ecuación son -2 y 3.
Concepto: ecuación simplificada donde el mayor exponente de la incógnita es 2.
Se dividen en
Incompletas: un coeficiente es cero.
Completas: ningún coeficiente es cero.
Ecuación de primer grado.
2. Problema:
Hallar un numero que sumado consigo mismo da 124.
El numero es x.
La suma del numero consigo mismo es x+x.
La ecuación: x+x=124
Al resolver la ecuación:
2x=124
x=(124)/2
x=62
Verificación:
(62) + (62)= 124
124=124
Ejemplo:
3x+2/3=7x+8
Incógnita→x
Coeficiente→3 y 7
Terminos independientes→2/3 y 8
Primer miembro→3x+2/3
Segundo miembro→7x+8
Concepto: expresión algebraica con una variable de exponente 1.
Elementos:
Términos independientes: números o fracciones que no acompañan a la incógnita.
Incógnita: letra que aparece en la ecuación
Coeficiente: números o fracciones que acompañan a la incógnita
Segundo miembro: todo a la derecha del signo igual.
Primer miembro: todo a la izquierda del signo igual.