ESCURRIMIENTO EN MEDIOS POROSOS
Captación de aguas subterráneas en régimen estable
Hidráulica de los pozos de captación (régimen estable)
Acuíferos Confinados
Acuíferos Libres
Hipótsis Simplificativas
Alimentación continúa, el caudal extraído mediante bombeo es igual al caudal que ingresa
El medio es homogéneo e isótropo.
La componente vertical de la velocidad es casi nula con relación a la componente horizontal
La ley de Darcy es aplicable
Superficies equipotenciales planas
El agua y el suelo del acuífero son incompresibles
Régimen permanente
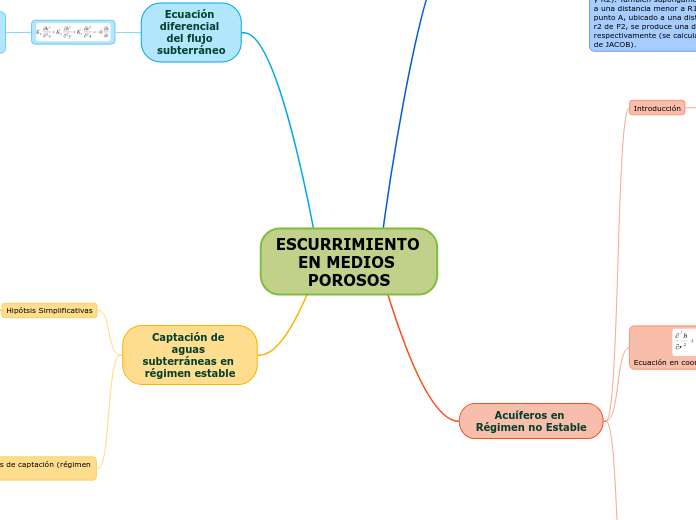
Ecuación diferencial del flujo subterráneo
Acuíferos en Régimen no Estable
Representación de soluciones
Recta descensos específicos en función del logaritmo de t/r^2
Recta descensos en función del logaritmo del 1/r^2
Se utilizan los datos obtenidos en un campo de pruebas con un pozo de extracción, a caudal constante, y con varios pozos de observación, para calcular los parámetros característicos T y S de un acuífero. Se obtiene una recta donde la variable es (1/r^2)
Recta descensos específicos en función del logaritmo del tiempo
Recta descensos en función del logaritmo del tiempo
Muestra la evolución de la extracción para un pozo de observación, situado a una distancia r del pozo de bombeo. Con los datos del ensayo de campo se aproxima a una recta.
Curva descensos en función del tiempo en coordenadas aritméticas
Ecuación en coordenadas polares planas
Integración (THEIS)
Solución
Solución de la integral exponencial (JACOB)
(hasta u<0,05)
Hipótesis
El caudal que entra al pozo es bombeado totalmente y vale Q, y matemáticamente queda expresado con la ecuación siguiente cuando x0 (cerca del pozo):
El agua bombeada es extraída de la formación y no vuelve a entrar en ella, y produce un descenso inmediato del nivel
El pozo de bombeo atraviesa todo el acuífero, siendo este último de espesor constante.
El pozo de bombeo tiene diámetro igual a cero, significa que el diámetro del pozo es despreciable en relación a las demás medidas lineales del problema.
El acuífero se extiende horizontalmente en todas las direcciones
El acuífero es homogéneo e isótropo en cuanto su permeabilidad. La permeabilidad es constante en todos los puntos, direcciones e instantes
Cuando la distancia de un punto al pozo, definida como la coordenada polar r, tiende a infinito la altura piezométrica dinámica h coincide con la altura piezométrica estática H
Introducción
Se analiza el comportamiento de los acuíferos a través del tiempo y el espacio considerando las magnitudes que intervienen y definen las características de un acuífero. Cuando la depresión en el pozo no llega a un valor estable a través del tiempo, para un caudal de bombeo constante, el acuífero no está equilibrado, no proporciona un caudal igual al extraído
Interferencia de pozos
Supongamos un acuífero con nivel piezométrico estático (NPE). En este se ubican dos pozos (P1 y P2) que bombean un caudal Q1 y Q2 y originan conos de depresión (NPD1 y NPD2) con radios de influencias (R1 y R2). Tambien supongamos que P2 se ubica a una distancia menor a R1+R2, y que en un punto A, ubicado a una distancia r1 de P1 y r2 de P2, se produce una depresión d1 y d2 respectivamente (se calcula con la ecuación de JACOB).
Concepto
Una perforación en explotación genera una depresión en el nivel piezométrico formando un “cono de depresión”. Llamaremos R al radio máximo de este cono (radio para el cual la depresión de los niveles piezométricos es cero). Si se perfora otro pozo, a una distancia menor que R el funcionamiento de ambos pozos interferirá en el desarrollo de cada cono de depresión ya que se interceptarán originando una depresión del nivel piezométrico dinámico mayor que la que producirían cada una de ellas por separado.
dT=d1+d2