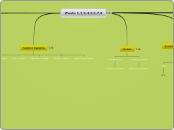
Weeks 1,2,3,4,5,6,7,8
Cartesian Product Context: characterized by finding all possible pairings between all possible pairings between 2 or more sets of objects.
Prime Factorization
Prime factorization is a factorization containing only prime numbers.
Fundamental Theorem of Arithmetic
Means you can't find more than one prime factorization for a number.
Number Theory
Prime numbers are only divisible by one and themselves.
Composite Numbers
Has a positive factor other than 1 and itself
Prime Numbers
Only divisible by 1 and itself
Even Numbers
Multiples of 2
Odd Numbers
An even number + 1
Subtraction Models/Contexts
Subtraction is characterized by starting with some initial quantity and removing a specified amount.
If aeW then a-o = o-a
Communative Property (doesn't always work)
If aeW and beW then a-b = b-a
Closure Property (doesn't always work)
If aeW and beW, then (a-b)eW
Multiplication Models/Contexts
Distributive Property: aeW, beW, ceW, then a(b+c) = ab+ac
Distributive Property
aeW, beW, ceW, then a(b+c) = ab+ac
Zero Property
aeW, oxa=o
Identity Property
aeW, 1xa=a, 1 is the identity element
Closure Property
If aeW and beW, then abeW
Communicative Property
If aeW and beW, then ab = ba
Associative Property (grouping)
(axb)xc = ax(bxc)
Division Models/Contexts
Divison Models/Contexts
Measurement
Characterized by using a given quantity to create groups(partitions) of a specified size(amount) and determining the # of groups that are formed.
Find: # of groups
Know: Quantity, and size of each group
Partition: Equal Sharing
Characterizing by distributing a given quantity among a specified number of groups(partition) and determining the size(amount) in each group(partition).
Find: Size of each group
Know: Quantity of #'s starting with, and # of groups
Addition
Identity Property of Division was probably the most difficult to understand.
Identity Property of Division of Whole Numbers
If aeW then a+o=a=o+a
Associative Property of Whole Numbers
If aeW, beW and ceW, then (a+b)+c=a+(b+c)=(a+c)+b
Communative Property of Whole Numbers
If aeW and beW then a+b=b+a
If aeX and beX then a+beX
Investigating Quantities
Cubes!
Bases
Units
1Unit
Longs
a^1
Flats
a^2
Cubes
a^3
Models
The Discrete Model is characterized by combining sets of two discrete objects.
Continuous Model
Measured Quantities
Discrete Model
Counted Quantities
Number Systems
The Mayan system is probably the most difficult number system to use.
Hindu-Arabic System
Roman System
Babylonian System
Myan System
Egyptian System
Tally System
Sets
Equivalent Sets and Equal sets are not always the same.
Venn Diagram
Equal Sets
Equivalent Sets
Complements
Conjoined Set
Universal Set
Sequences
Geometric Sequences are sequences of numbers with a common ratio; that is, if you form the ratio of any two consecutive terms in the sequence the ratio is the same.
Recurrence Relationship Sequence
Geometric Sequence
Arithmetic Sequence
Problem Solving
Don't forget to read over the problem over a second time so that you understand what you're reading.
Implement you Plan
Devise A Plan
Understand the Problem
Fractions
Cuisennaire rods were an interesting manipulative to use to comprehend fractions.
Use of Cuisennaire Rods
Any number that can be expressed as the quotient of two integers. a/b
Ratios
Comparing 2 separate things
Division
Separating groups
Interpretations of a fraction
Copies
Part-Whole interpretation
Multiplication of fractions
An area model is best used as a table.
Area Model
Division of fractions
When using the partition model it's most important to know the # of groups as well as the size.
Partition
Repeated Subtraction
Ratio
Example of ratio:
2:3
Comparing two quantities regardless of whether units are the same.
Proportion
a/b = c/d
Where two ratios are equal.
Proportional Reasoning
Relative thinking: identifying relationships between two quantities and comparing them.
Relative thinking.
Recognition of quantities and how they change
Rational Numbers
Ratio Sense
Utilizing
Properties of Modular Arithmatic(Addition)
Commutative Property of Addition:
a+b(mod 5)=b+a(mod 5)
Identity Property of Addition
Communative Property of Addition
Closure Property of Addition
Properties of Modular Arithmatic(Multiplication)
Commutative Property of multiplication:
axb(mod 5)=bxa(mod 5)
Inverse Property of Multiplication
Identity Property of Multiplication
Commutative Property of Multiplication
Closure Property of Multiplication
Investigating Quantity
This is the last topic of the course! Hooray!!
Percents
Decimals
Multiplication of integers
Subtraction of integers
Addition of integers