Medidas de dispersión
Coeficiente de Variación
CV = desviación estándar / media aritmética x 100
Fórmula del coeficiente de variación
Su cálculo se obtiene de dividir la desviación típica entre el valor absoluto de la media del conjunto y por lo general se expresa en porcentaje para su mejor comprensión.
X: variable sobre la que se pretenden calcular la varianza
σx: Desviación típica de la variable X.
| x̄ |: Es la media de la variable X en valor absoluto con x̄ ≠ 0
El coeficiente de variación se puede ver expresado con las letras CV o r, dependiendo del manual o la fuente utilizada.
El coeficiente de variación se utiliza para comparar conjuntos de datos pertenecientes a poblaciones distintas.
El coeficiente de variación, también denominado como coeficiente de variación de Pearson, es una medida estadística que nos informa acerca de la dispersión relativa de un conjunto de datos.
Es decir, nos informa al igual que otras medidas de dispersión, de si una variable se mueve mucho, poco, más o menos que otra.
Desviación poblacional
Las fórmulas para calcular estas dos desviaciones estándar son casi idénticas:
Calcule la media.
Reste la media de cada valor para obtener desviaciones de la media.
Cuadre cada una de las desviaciones.
Sume todas estas desviaciones cuadradas.
Ahora el cálculo de estas desviaciones estándar es diferente:
Si estamos calculando la desviación estándar de la población, dividimos entre n, el número de valores de datos.
Si estamos calculando la desviación estándar de la muestra, dividimos entre n -1, uno menos que el número de valores de datos.
El paso final, en cualquiera de los dos casos que estamos considerando, es sacar la raíz cuadrada del cociente del paso anterior.
Cuanto mayor sea el valor de n , más cerca estarán las desviaciones estándar de la población y la muestra.
La desviación estándar de la población es un parámetro, que es un valor fijo calculado a partir de cada individuo de la población.
Una desviación estándar de muestra es una estadística. Esto significa que se calcula solo a partir de algunos de los individuos de una población.
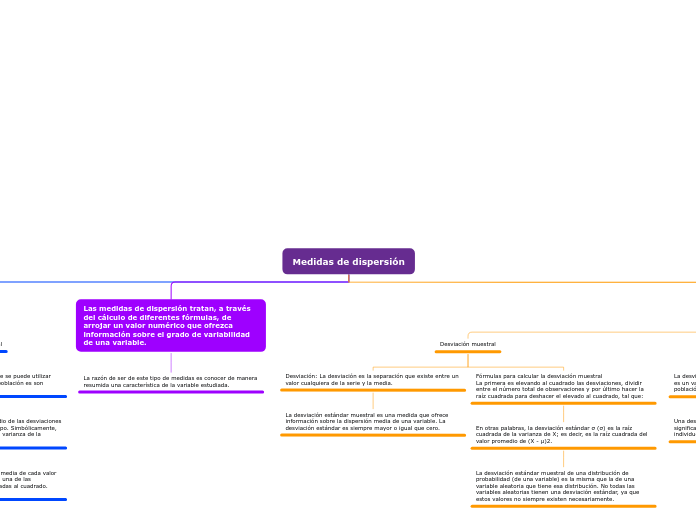
Desviación muestral
Fórmulas para calcular la desviación muestral
La primera es elevando al cuadrado las desviaciones, dividir entre el número total de observaciones y por último hacer la raíz cuadrada para deshacer el elevado al cuadrado, tal que:
En otras palabras, la desviación estándar σ (σ) es la raíz cuadrada de la varianza de X; es decir, es la raíz cuadrada del valor promedio de (X - μ)2.
La desviación estándar muestral de una distribución de probabilidad (de una variable) es la misma que la de una variable aleatoria que tiene esa distribución. No todas las variables aleatorias tienen una desviación estándar, ya que estos valores no siempre existen necesariamente.
Desviación: La desviación es la separación que existe entre un valor cualquiera de la serie y la media.
La desviación estándar muestral es una medida que ofrece información sobre la dispersión media de una variable. La desviación estándar es siempre mayor o igual que cero.
Las medidas de dispersión tratan, a través del cálculo de diferentes fórmulas, de arrojar un valor numérico que ofrezca información sobre el grado de variabilidad de una variable.
La razón de ser de este tipo de medidas es conocer de manera resumida una característica de la variable estudiada.
Principales medidas de dispersión
Varianza poblacional
El análisis de varianza es una técnica que se puede utilizar para decidir si las medias de dos o más población es son iguales.
La varianza de una muestra es el promedio de las desviaciones elevadas al cuadrado de la media del grupo. Simbólicamente, estos representa de la siguiente manera: varianza de la muestra=s2=xi-x2n-1
1)Calcular la media muestral 2)Restar la media de cada valor de la muestra. 3)Elevar al cuadrado cada una de las diferencias. 4)Sumar las diferencias elevadas al cuadrado. 5)Dividir entren-1
varianza muestral
Su formula matemática para el caso de datos referentes a una muestra es: σ² = (Σ x²) / N ) - μ².
X → Variable sobre la que se pretenden calcular la varianza
xi → Observación número i de la variable X. i puede tomará valores entre 1 y n.
N → Número de observaciones.
x̄ → Es la media de la variable X.
Se puede definir como el "casi promedio" de los cuadrados de las desviaciones de los datos con respecto a la media muestral.
Rango
Su fórmula es:
R = Máxx – Mínx
Donde:
R → Es el rango.
Máx → Es el valor máximo de la muestra o población.
Mín → Es el valor mínimo de la muestra o población estadística.
x → Es la variable sobre la que se pretende calcular esta medida.
El rango es un valor numérico que indica la diferencia entre el valor máximo y el mínimo de una población o muestra estadística.