por Rafael Corrêa da Silva hace 5 años
1504
Progressão Geométrica
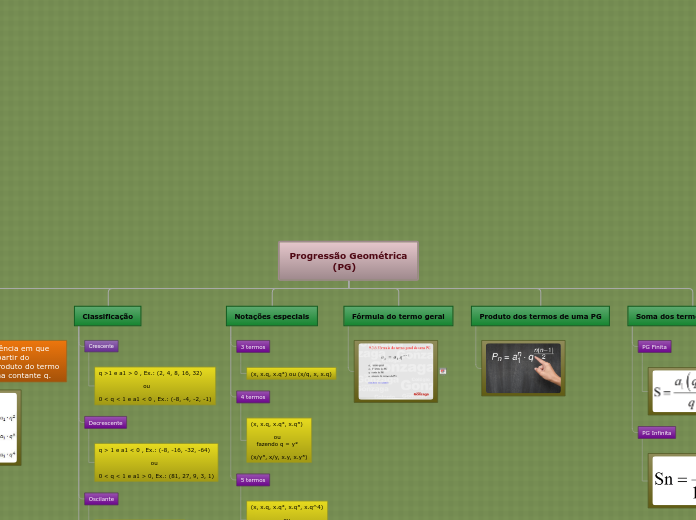
Uma progressão geométrica é uma sequência numérica onde cada termo, a partir do segundo, resulta do produto do termo anterior por uma constante chamada de razão (q). As progressões geométricas podem ser classificadas como decrescentes, crescentes, oscilantes, constantes ou estacionárias, dependendo do valor da razão e do primeiro termo.